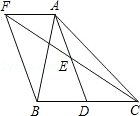
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF. 
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
参考答案:
【答案】
(1)证明:
∵AF∥BC,
∴∠AFE=∠DCE,
∵E是AD的中点,
∴AE=DE,
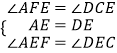 ,
,
∴△AEF≌△DEC(AAS),
∴AF=DC,
∵AF=BD,
∴BD=CD
(2)证明:四边形AFBD是矩形.
理由:
∵AB=AC,D是BC的中点,
∴AD⊥BC,
∴∠ADB=90°
∵AF=BD,
∵过A点作BC的平行线交CE的延长线于点F,即AF∥BC,
∴四边形AFBD是平行四边形,
又∵∠ADB=90°,
∴四边形AFBD是矩形.
【解析】(1)先由AF∥BC,利用平行线的性质可证∠AFE=∠DCE,而E是AD中点,那么AE=DE,∠AEF=∠DEC,利用AAS可证△AEF≌△DEC,那么有AF=DC,又AF=BD,从而有BD=CD;(2)四边形AFBD是矩形.由于AF平行等于BD,易得四边形AFBD是平行四边形,又AB=AC,BD=CD,利用等腰三角形三线合一定理,可知AD⊥BC,即∠ADB=90°,那么可证四边形AFBD是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】乘法公式的探究及应用.
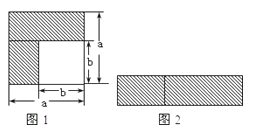
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 面积是 (写成多项式乘法的形式);
(3)比较图1、图2阴影部分的面积,可以得到公式 ;
(4)运用你所得到的公式,计算下列各题:
①10.2×9.8,②(2m+n﹣p)(2m﹣n+p). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,DE⊥AB.

(1)求∠ABC的度数;
(2)如果 ,求DE的长.
,求DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是( )
A.0既不是正数,也不是负数
B.1是绝对值最小的数
C.一个有理数不是整数就是分数
D.0的绝对值是0 -
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2,沿x轴向左平移1个单位后,得到的物线的解析式是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中,正确的是( )
A.(a3)4=a12
B.a3a5=a15
C.a2+a2=a4
D.a6÷a2=a3 -
科目: 来源: 题型:
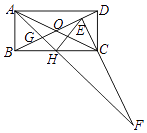
查看答案和解析>>【题目】如图,矩形ABCD中,BC=2AB,对角线相交于O,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列5个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四边形GHCE , ⑤CF=BD.正确的有( )个.
A.1
B.2
C.3
D.4
相关试题

