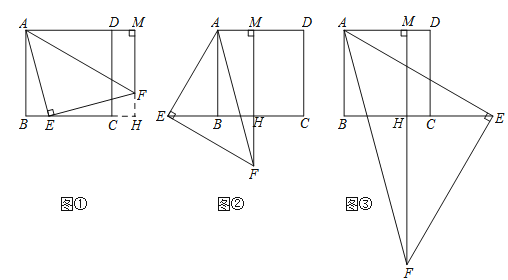
【题目】已知四边形ABCD是正方形，等腰直角△AEF的直角顶点E在直线BC上（不与点B，C重合），FM⊥AD，交射线AD于点M．

（1）当点E在边BC上，点M在边AD的延长线上时，如图①，求证：AB+BE=AM；

（提示：延长MF，交边BC的延长线于点H．）

（2）当点E在边CB的延长线上，点M在边AD上时，如图②；当点E在边BC的延长线上，点M在边AD上时，如图③．请分别写出线段AB，BE，AM之间的数量关系，不需要证明；

（3）在（1），（2）的条件下，若BE=，∠AFM=15°，则AM= ．

参考答案：

【答案】（1）证明见试题解析；（2）BE= AM+AB；（3）或．

【解析】

试题分析：（1）由等腰直角三角形的性质和正方形的性质得到AE=EF，∠ABE=∠EHF=90°，得到△ABE≌△EHF，即可得到结论；

（2）同（1）先证明△ABE≌△EHF，再利用全等三角形的性质定理可得结论；

（3）分三种情况讨论，首先由∠AFM=15°，易得∠EFH，由△ABE≌△EHF，根据全等三角形的性质易得∠AEB，利用锐角三角函数易得AB，利用（1）（2）的结论，易得AM．

试题解析：（1）如图①，延长MF，交边BC的延长线于点H，∵四边形ABCD是正方形，FM⊥AD，∴∠ABE=90°，∠EHF=90°，四边形ABHM为矩形，∴AM=BH=BE+EH

∵△AEF为等腰直角三角形，∴AE=AF，∠AEB+∠FEH=90°，∵∠EFH+∠FEH=90°，∴∠AEB=∠EFH，在△ABE与△EHF中，∵∠ABE=∠EHF=90°，∠ABE=∠EHF=90°，∠AEB=∠EFH，AE=EF，∴△ABE≌△EHF（AAS），∴AB=EH，∵AM=BH=BE+EH，∴AM=BE+AB，即AB+BE=AM；

（2）BE= AM+AB．理由如下：

如图②，∵∠AEB+∠FEH=90°，∠AEB+∠EAB=90°，∴∠FEH=∠EAB，在△ABE与△EHF中，∵∠ABE=∠EHF，∠EAB=∠FEH，AE=FE，∴△ABE≌△EHF（AAS），∴AB=EH=EB+AM；

如图③∠BAE+∠AEB=90°，∠AEB+∠HEF=90°，∴∠BAE=∠HEF，在△ABE与△EHF中，∵∠ABE=∠EHF，∠BAE=∠HEF，AE=FE，∴△ABE≌△EHF（AAS），∴AB=EH，∴BE=BH+EH=AM+AB；

（3）如图①，∵∠AFM=15°，∠AFE=45°，∴∠EFM=60°，∴∠EFH=120°，在△EFH中，∵∠FHE=90°，∠EFH=120°，∴此情况不存在；

如图②，∵∠AFM=15°，∠AFE=45°，∴∠EFH=60°，∵△ABE≌△EHF，∴∠EAB=∠EFH=60°，∵BE=，∴AB=BEtan60°==3，∵AB=EB+AM，∴AM=AB﹣EB=；

如图③，∵∠AFM=15°，∠AFE=45°，∴∠EFH=45°﹣15°=30°，∴∠AEB=30°，∵BE=，∴AB=BEtan30°==1，∵BE=AM+AB，AM=BE﹣AB=，故答案为：或．

关闭