Question

【题目】已知，AB是半圆O的直径，弦CD∥AB，动点M、N分别在线段OC、CD上，AM的延长线与射线ON相交于点E，与弦CD相交于点F．
（1）如图1，若DN=OM，求证：AM=ON；

（2）如图2，点P是弦CD上一点，若AP=OP，∠APO=90°，求∠COP的度数；

（3）在（1）的条件下，若AB=20，cos∠AOC= ，当点E在ON的延长线上，且NE=NF时，求线段EF的长．

Answer 1

【答案】
（1）解：如图1，

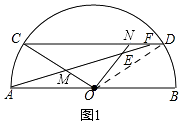
连接OD，

∴OA=OD，

∵CD∥AB，

∴∠BOD=∠NDO， ，

∴∠AOC=∠BCD，

∴∠AOC=∠CDO，

在△AMO和△OND中， ，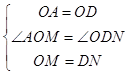

∴△AMO≌△OND，

∴AM=ON，

（2）解：如图2，

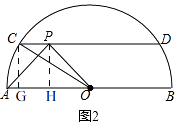
过点C作CG⊥AB，PH⊥AB，

∴CG=PH，

∵AP=OP，∠APO=90°，

∴∠AOP=45°，PH= OA，

∴CG= OA= OC，

∴∠AOC=30°，

∴∠COP=∠AOP﹣∠AOC=15°

（3）解：如图3，

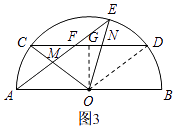
作OG⊥CD于G，连接OD，

∵AB=20，

∴OC=10

CG=OCcos∠C=OCcos∠AOC=10× =8

∴CD=2CG=16

∵NE=NF，

∴∠E=∠EFN

∵CD∥AB，

∴∠EFN=∠A

∴∠E=∠A，

∴OE=OA

∵CD∥AB，

∴∠BOD=∠D=∠C=∠AOC

∴∠AOE=∠COD

∴△AOE≌△COD，

∴AE=CD=16

∵△AOM≌△ODN，

∴∠NOD=∠A=∠E

∴AE∥OD，

∴四边形AODF是平行四边形

∴AF=OD=10

∴EF=AE﹣AF=16﹣10=6

【解析】（1）先判断出∠BOD=∠NDO， 进而得出∠AOC=∠CDO，即可得出△AMO≌△OND，结论得证；（2）构造出直角三角形，先判断出PH= OA，即可得出CG= OC，进而求出∠AOC=30°，最后用角的差，即可得出结论．（3）先求出CD=2CG=16，再判断出△AOE≌△COD，进而判断出四边形AODF是平行四边形，最后用线段的差即可得出结论；