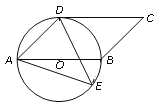
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45.
(1)试判断CD与⊙O的位置关系,并证明你的结论;
(2)若⊙O的半径为3,sin∠ADE=![]() ,求AE的值.
,求AE的值.
参考答案:
【答案】(1)CD与圆O相切,证明见解析;(2)AE=5 .
【解析】(1)连接OD,则∠AOD=为直角,由四边形ABCD是平行四边形,则AB∥CD,从而得出∠CDO=90°,即可证出答案.
(2)连接BE,则∠ADE=∠ABE,根据题意得sin∠ABE=![]() . 由AB是圆O的直径求出AB的长.再在Rt△ABE中,求得AE即可.
. 由AB是圆O的直径求出AB的长.再在Rt△ABE中,求得AE即可.
解:(1)CD与圆O相切. 证明:连接OD,则∠AOD=2∠AED =2×450=900.
∵四边形ABCD是平行四边形,∴AB//DC.∴∠CDO=∠AOD=90°.∴OD⊥CD. ∴CD与圆O相切
(2)连接BE,则∠ADE=∠ABE. ∴sin∠ADE=sin∠ABE=![]() .
.
∵AB是圆O的直径,∴∠AEB=900,AB=2×3=6.
在Rt△ABE中,sin∠ABE=![]() .∴AE=5 .
.∴AE=5 .
“点睛”此题考查了切线的判定、圆周角定理、垂线定理、平行四边形的性质以及三角函数等知识.此题综合性较强,难度适中,注意掌握辅助线的作法,注意数形结合思想与转化思想的应用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:P是正方形ABCD对角线BD上一点,PE⊥DC,PF⊥BC,E、F分别为垂足.
求证:AP=EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在两个不透明的口袋中分别装有三个颜色分别为红色、白色、绿色的小球,这三个小球除颜色外其它都相同.
(1)在其中一个口袋中一次性随机摸出两个球.请写出在这一过程中的一个必然事件;
(2)若分别从两袋中随机各取出一个小球,试求取出两个小球颜色相同的概率(用列表法或画树状图).
-
科目: 来源: 题型:
查看答案和解析>>【题目】由于提倡环保节能,自行车已成为市民日常出行的主要工具之一,据某自行车经销店4至6月份统计,某品牌自行车4月份销售200辆,6月份销售338辆,求该品牌自行车销售量的月平均增长率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学现有学生2870人,学校为了进一步丰富学生课余生活,组织调查各兴趣小组活动情况,为此校学生会进行了一次随机抽样调查.根据采集到的数据,绘制如下两个统计图(不完整):
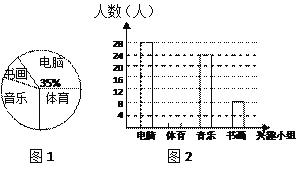
请你根据统计图1、2中提供的信息,解答下列问题:
(1)写出2条有价值信息(不包括下面要计算的信息);
(2)这次抽样调查的样本容量是多少?在图2中,请将条形统计图中的“体育”部分的图形补充完整;
(3)爱好“书画”的人数占被调查人数的百分数是多少?估计该中学现有的学生中,爱好“书画”的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、C、E是同一直线上的三点,四边形ABCD与四边形CEFG都是正方形,连接BG、DE.
(1)求证:BG=DE;
(2)已知小正方形CEFG的边长为1cm,连接CF,如果将正方形CEFG绕点C逆时针旋转,当A、E两点之间的距离最小时,求线段CF所扫过的面积.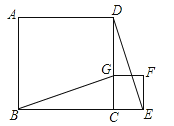
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程组
(1)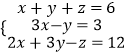
(2)
相关试题

