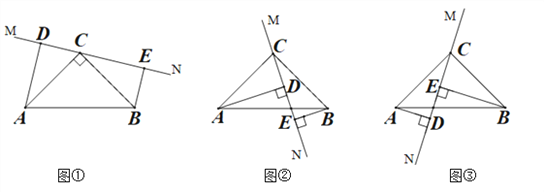
【题目】在△ABC中,∠ACB=90,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图①位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图②位置时,试问:DE,AD,BE有怎样的等量关系?请写出这个等量关系,并加以证明.
(3)当直线MN绕点C旋转到图③位置时,DE,AD,BE之间的等量关系是 (直接写出答案,不需证明.)
参考答案:
【答案】(1)证明见解析;(2)AD-BE=DE,证明见解析;(3)BE-AD=DE.
【解析】试题分析:
(1)由已知条件易证∠DAC和∠DCA互余,∠ECB和∠DCA互余,由此可得∠DAC=∠ECB,结合题中其它条件证△ADC和△CEB全等可得AD=CE,CD=BE,就可证得:DE=DC+CE=AD+BE;
(2)由(1)中思路证△ADC和△CEB全等可得AD=CE,CD=BE,从而可得:DE=CE-CD=AD-BE;
(3)同(2)中思路证△ADC和△CEB全等可得AD=CE,CD=BE,从而可得:DE=CD-CE=BE-AD.
试题解析:
(1)∵AD⊥MN于D,BE⊥MN于E,
∴∠ADC=∠CEB=90°,
又∵∠ACB=90°,
∴∠DAC+∠ACD=90°,∠ECB+∠ACD=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中: 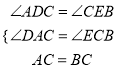 ,
,
∴△ADC≌△CEB,
∴AD=CE,DC=BE,
又∵DE=DC+CE,
∴DE=AD+BE.
(2)如图②,DE,AD,BE的关系为:DE=AD-BE.理由如下:
∵AD⊥MN于D,BE⊥MN于E,
∴∠ADC=∠CEB=90°,
又∵∠ACB=90°,
∴∠DAC+∠ACD=90°,∠ECB+∠ACD=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中:  ,
,
∴△ADC≌△CEB,
∴AD=CE,DC=BE,
又∵DE=CE-CD,
∴DE=AD-BE.
(3)如图③,DE,AD,BE之间的等量关系是:DE=BE-AD,理由如下:
∵AD⊥MN于D,BE⊥MN于E,
∴∠ADC=∠CEB=90°,
又∵∠ACB=90°,
∴∠DAC+∠ACD=90°,∠ECB+∠ACD=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中:  ,
,
∴△ADC≌△CEB,
∴AD=CE,DC=BE,
又∵DE=CD-CE,
∴DE=BE-AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着“一带一路”的建设推进,我国与一带一路沿线部分地区的贸易额加速增长.据统计,2017年我国与东南亚地区的贸易额将超过189 000 000万美元.将189 000 000用科学记数法表示应为( )
A. 189×106 B. 1.89×106 C. 18.9×107 D. 1.89×108
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的高AD、BF相交于点E,AD=BD,BC=6cm,DC=2cm,
(1)求证:△BDE≌△ADC;(2)求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与半径为2的⊙O相切于点C,点D、E、F是⊙O上三个点,EF∥AB,若EF=
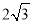 ,则∠EDC的度数为( )
,则∠EDC的度数为( )
A. 60° B. 90° C. 30° D. 75°
-
科目: 来源: 题型:
查看答案和解析>>【题目】设MN是线段AB的垂直平分线,当点P在MN上运动时,PA,PB的长度都随之变化,但总保持______
-
科目: 来源: 题型:
查看答案和解析>>【题目】2015年4月25日,尼泊尔发生了里氏8.1级地震,某中学组织了献爱心捐款活动,该校教学兴趣小组对本校学生献爱心捐款额做了一次随机抽样调查,并绘制了不完整的频数分布表和频数分布直方图(每组含前一个边界值,不含后一个边界值).如图所示:
捐款额(元)
频数
百分比
0≤x<5
5
10%
10≤x<15
a
20%
15≤x<20
15
30%
20≤x<25
14
b
25≤x<30
6
12%
总计
100%
(1)a等于多少?b等于多少?
(2)补全频数分布直方图;
(3)该校共有1600名学生,估计这次活动中爱心捐款额不低于20元的学生有多少人?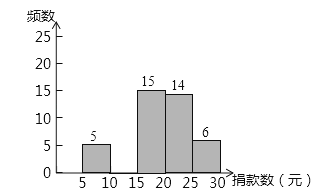
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中,正确的是( )
A. 5a2b﹣4a2b=a2b B. a+b=ab C. 6a3﹣2a3=4 D. 2b2+3b3=5b5
相关试题

