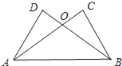
【题目】如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
求证:△OAB是等腰三角形.
参考答案:
【答案】详见解析.
【解析】
利用HL定理得出△ABD≌BAC即可得出∠DBA=∠CAB,再利用等腰三角形的判定得出即可.
证明:
∵AC⊥BC,BD⊥AD
∴∠D=∠C=90°,
在Rt△ABD和Rt△BAC中,
![]() ,
,
∴Rt△ABD≌Rt△BAC(HL),
∴∠DBA=∠CAB,
∴OA=OB,
即△OAB是等腰三角形.
另外一种证法:
证明:∵AC⊥BC,BD⊥AD
∴∠D=∠C=90°
在Rt△ABD和Rt△BAC中
![]()
∴Rt△ABD≌Rt△BAC(HL)
∴AD=BC,
在△AOD和△BOC中
![]() ,
,
∴△AOD≌△BOC(AAS),
∴OA=OB,
即△OAB是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCO放在平面直角坐标系中,其中顶点B的坐标为(5,3),E是BC边上一点,将△ABE沿AE翻折,点B刚好与OC边上的点D重合,过点E的反比例函数y=
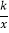 的图象与边AB交于点F,则线段AF的长为_____.
的图象与边AB交于点F,则线段AF的长为_____.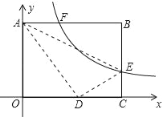
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,有一条长为10的线段AB,其端点A、点B分别在y轴、x轴上滑动,点C为以AB为直径的⊙D上一点(C始终在第一象限),且tan∠BAC=
 .则当点A从A0(0,10)滑动到O(0,0),B从O(0,0)滑动到B0(10,0)的过程中,点C运动的路径长为_____.
.则当点A从A0(0,10)滑动到O(0,0),B从O(0,0)滑动到B0(10,0)的过程中,点C运动的路径长为_____.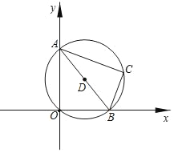
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为等边三角形ABC内的一点,且P到三个顶点A,B,C的距离分别为3,4,5,则△ABC的面积为( )
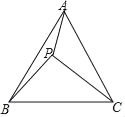
A.
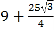 B.
B. 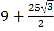 C.
C. 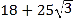 D.
D. 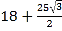
-
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的宜兴﹣我最喜爱的宜兴小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图.
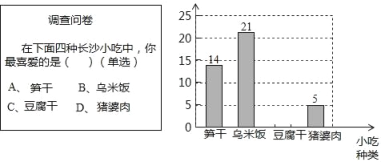
请根据所给信息解答以下问题
(1)请补全条形统计图;
(2)若全校有1000名同学,请估计全校同学中最喜爱“笋干”的同学有多少人?
(3)在一个不透明的口袋中有4个元全相同的小球,把它们分别标号为四种小吃的序号A,B,C,D,随机地把四个小球分成两组,每组两个球,请用列表或画树状图的方法,求出A,B两球分在同一组的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】宜兴在“创建文明城市”行动中,某社区计划对面积为2160m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为480m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积;
(2)设甲工程队施工x天,乙工程队施工y天,刚好完成绿化任务,求y与x的函数表达式;
(3)若甲队每天绿化费用是0.8万元,乙队每天绿化费用为0.35万元,且甲、乙两队施工的总天数不超过26天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点A(1,﹣
 ),点B(﹣2,n)在抛物线y=ax2(a≠0)上.
),点B(﹣2,n)在抛物线y=ax2(a≠0)上.(1)求a的值与点B的坐标;
(2)将抛物线y=ax2(a≠0)平移,记平移后点A的对应点为A′,点B的对应点为B',若四边形ABB′A′为正方形,求平移后的抛物线的解析式.
相关试题

