【题目】如图在直角坐标系中，四边形ABCO为正方形，A点的坐标为（a，0），D点的坐标为（0，b），且a，b满足（a﹣3）2+|b﹣|＝0．

（1）求A点和D点的坐标；

（2）若∠DAE＝∠OAB，请猜想DE，OD和EB的数量关系，说明理由．

（3）若∠OAD＝30°，以AD为三角形的一边，坐标轴上是否存在点P，使得△PAD为等腰三角形，若存在，直接写出有多少个点P，并写出P点的坐标，选择一种情况证明．

参考答案：

【答案】（1）D（0，），A（3，0）；（2）DE＝OD+EB； 理由见解析；（3）点P的坐标为：∴P（﹣3，0）或（0，3）或（0，﹣）或（1，0）或（3+2，0）或（3﹣2，0）．证明见解析.

【解析】

(1)根据完全平方式和绝对值的非负性确定a,b的值，从而求点的坐标；

（2）在CO的延长线上找一点F，使OF＝BE，连接AF，通过△AOF≌△ABE，得到AF＝AE，∠OAF＝∠BAE，等量代换得到∠DAF＝∠EAD，进而证明△AFD≌△AED，从而求解；

（3）分三种情形讨论求解：AD=DP或AD=AP或PD=AP，分别画图根据AD和OA的长确定点P的坐标．

（1）∵（a﹣3）2+|b﹣|＝0，

∴a＝3，b＝，

∴D（0，），A（3，0）；

（2）DE＝OD+EB； 理由如下：

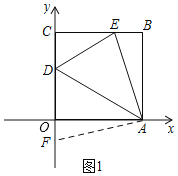
如图1，在CO的延长线上找一点F，使OF＝BE，连接AF，

在△AOF和△ABE中， ，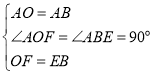

∴△AOF≌△ABE（SAS），

∴AF＝AE，∠OAF＝∠BAE，

又∵∠OAB＝90°，∠DAE＝，

∴∠BAE+∠DAO＝45°，

∴∠DAF＝∠OAF+∠DAO＝45°，

∴∠DAF＝∠EAD，

在△AFD和△AED中， ，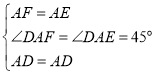

∴△AFD≌△AED（SAS），

∴DF＝DE＝OD+EB；

（3）有3种情况共6个点：

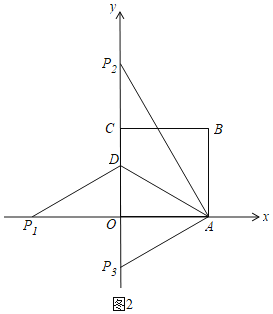
①当DA＝DP时，如图2，

Rt△ADO中，OD＝，OA＝3，

∴AD＝，

∴P1（﹣3，0），P2（0，3），P3（0，﹣）；

②当AP4＝DP4时，如图3，

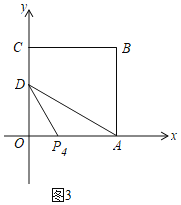
∴∠ADP4＝∠DAP4＝30°，

∴∠OP4D＝60°，

Rt△ODP4中，∠ODP4＝30°，OD＝，

∴OP4＝1，

∴P4（1，0）；

③当AD＝AP时，如图4，

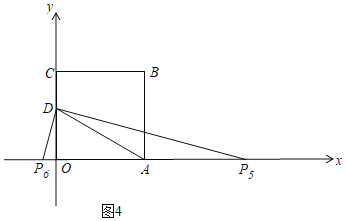
∴AD＝AP5＝AP6＝2，

∴P5（3+2，0），P6（3﹣2，0），

综上，点P的坐标为：∴P（﹣3，0）或（0，3）或（0，﹣）或（1，0）或（3+2，0）或（3﹣2，0）．

证明：P5（3+2，0），

∵∠OAD＝30°且△ADO是直角三角形，

又∵AO＝3，DO＝，

∴DA＝2，

而P5A＝|3+2﹣3|＝2，

∴P5A＝DA，

∴△P5AD是等腰三角形．

关闭