【题目】如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处;
(1)求证:B′E=BF;
(2)设AE=a,AB=b,BF=C,试猜想a,b,c之间的一种关系,并给予证明.

参考答案:
【答案】(1)证明见解析;
(2)a,b,c三者存在的关系是a+b>c,理由见解析.
【解析】(1)首先根据题意得B′F=BF,∠B′FE=∠BFE,接着根据平行线的性质和等腰三角形的判定即可证明B′E=BF;
(2)解答此类题目时要仔细读题,根据三角形三边关系求解分类讨论解答,要提高全等三角形的判定结合勾股定理解答.
证明:(1)由题意得B′F=BF,∠B′FE=∠BFE,
在矩形ABCD中,AD∥BC,
∴∠B′EF=∠BFE,
∴∠B′FE=∠B'EF,
∴B′F=BE,
∴B′E=BF;
解:(2)答:a,b,c三者关系不唯一,有两种可能情况:
(ⅰ)a,b,c三者存在的关系是a2+b2=c2.
证明:连接BE,则BE=B′E,
由(1)知B′E=BF=c,
∴BE=c.
在△ABE中,∠A=90°,
∴AE2+AB2=BE2,
∵AE=a,AB=b,
∴a2+b2=c2;
(ⅱ)a,b,c三者存在的关系是a+b>c.
证明:连接BE,则BE=B′E.
由(1)知B′E=BF=c,
∴BE=c,
在△ABE中,AE+AB>BE,
∴a+b>c.
“点睛”此题以证明和探究结论形式来考查矩形的翻折、等角对等边、三角形全等、勾股定理等知识.第一,较好考查学生表述数学推理和论证能力,第(1)问重点考查了学生逻辑推理的能力,主要利用等角对等边、翻折等知识来证明;第二,试题呈现显示了浓郁的探索过程,试题设计的起点低,图形也很直观,也可通过自已动手操作,寻找几何元素之间的对应关系,形成较为常规的方法解决问题,第(2)问既考查了学生对勾股定理掌握的程度又考查学生的数学猜想和探索能力,这对于培养学生创新意识和创新精神十分有益;第三,解题策略多样化在本题中得到了充分的体现.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的是( )
A.平分弦的直径垂直于弦;
B.与直径垂直的直线是圆的切线;
C.对角线互相垂直的四边形是菱形;
D.连接等腰梯形四边中点的四边形是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点M(2+x,9﹣x2)在x轴的负半轴上,则点M的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】金砖五国成员国巴西的首都巴西利亚、新西兰的首都惠灵顿与北京的时差如下表:
城市
惠灵顿
巴西利亚
时差/h
+4
﹣11
若现在的北京时间是11月16日8:00,请从A,B两题中任选一题作答.
A.那么,现在的惠灵顿时间是11月_____日_____
B.那么,现在的巴西利亚时间是11月_____日_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验室里,水平桌面上有甲、乙、丙三个相 同高度的圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在10cm高度处连通(即管子底部离容器底10cm),现三个容器中,只有乙中有水,水位高4cm,如图所示.若每分钟同时向甲和丙注入相同量的水,开始注水1分钟,甲的水位上升3cm.则开始注入 分钟水量后,甲的水位比乙高1cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(1)这两次各购进这种衬衫多少件?
(2)若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于1950元,则第二批衬衫每件至少要售多少元?
-
科目: 来源: 题型:
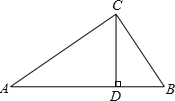
查看答案和解析>>【题目】如图,在△ABC中,CD是AB边上高,若AD=16,CD=12,BD=9.
(1)求△ABC的周长;
(2)判断△ABC的形状并加以证明.
相关试题

