【题目】如图,OB平分∠CBA,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=18,则△AMN的周长为( )

A.30 B.33 C.36 D.39
参考答案:
【答案】A.
【解析】
试题分析:根据BO平分∠CBA,CO平分∠ACB,且MN∥BC,可得出MO=MC,NO=NB,所以三角形AMN的周长是AB+AC.
解:∵BO平分∠CBA,CO平分∠ACB,
∴∠NBO=∠OBC,∠OCM=∠OCB,
∵MN∥BC,
∴∠NOB=∠OBC,∠MOC=∠OCB,
∴∠NBO=∠NOB,∠MOC=∠MCO,
∴MO=MC,NO=NB,
∵AB=12,AC=18,
∴△AMN的周长=AM+MN+AN=AB+AC=12+18=30.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】要从甲、乙两名运动员中选出一名参加“2016里约奥运会”100m比赛,对这两名运动员进行了10次测试,经过数据分析,甲、乙两名运动员的平均成绩均为10.05(s),甲的方差为0.024(s2),乙的方差为0.008(s2),则这10次测试成绩比较稳定的是 运动员.(填“甲”或“乙”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某校女子排球队队员的年龄分布
年龄/岁
13
14
15
16
频数
1
1
7
3
则该校女子排球队队员的平均年龄是 岁.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角∠A是120°,第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C的大小是( )
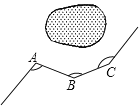
A.150° B.130° C.140° D.120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形OABC的顶点O在坐标系原点,顶点A在x轴上,∠B=120°,OA=2,将菱形OABC绕原点O顺时针旋转105°至OA′B′C′的位置,则点B′的坐标为( )
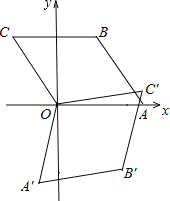
A.(﹣
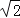 ,
,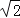 ) B.(
) B.(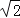 ,﹣
,﹣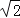 )
) C.(2,﹣2) D.(
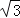 ,﹣
,﹣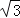 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ADF和△BCE中,∠A=∠B,点D、E、F、C在同﹣直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF。
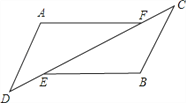
(1)请用其中两个关系式作为条件,另一个作为结论,写出所有你认为正确的命题.(用序号写出命题书写形式,如:如果①、②,那么③)
(2)选择(1)中你写出的一个命题,说明它正确的理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:| 2-x | + | y +3| = 0,则x-y =_______________ .
相关试题

