【题目】(10分)如图①,将两块全等的三角板拼在一起,其中△ABC的边BC在直线l上,AC⊥BC且AC = BC;△EFP的边FP也在直线l上,边EF与边AC重合,EF⊥FP且EF = FP。
(1)在图①中,请你通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系;
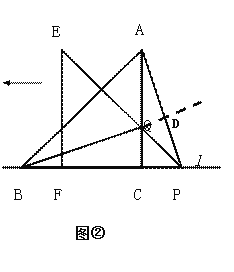
(2)将三角板△EFP沿直线l向左平移到图②的位置时,EP交AC于点Q,连接AP、BQ。猜想并写出BQ与AP所满足的数量关系和位置关系,并证明你的猜想;
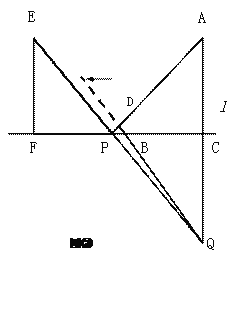
(3)将三角板△EFP沿直线l向左平移到图③的位置时,EP的延长线交AC的延长线于点Q,连接AP、BQ。你认为(2)中猜想的BQ与AP所满足的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由。

参考答案:
【答案】略
【解析】如图①,将两块全等的三角板拼在一起,其中△ABC的边BC在直线l上,AC⊥BC且AC = BC;△EFP的边FP也在直线l上,边EF与边AC重合,EF⊥FP且EF = FP。
(1)在图①中,请你通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系;
(2)将三角板△EFP沿直线l向左平移到图②的位置时,EP交AC于点Q,连接AP、BQ。猜想并写出BQ与AP所满足的数量关系和位置关系,并证明你的猜想;
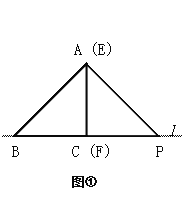 (3)将三角板△EFP沿直线l向左平移到图③的位置时,EP的延长线交AC的延长线于点Q,连接AP、BQ。你认为(2)中猜想的BQ与AP所满足的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由。
(3)将三角板△EFP沿直线l向左平移到图③的位置时,EP的延长线交AC的延长线于点Q,连接AP、BQ。你认为(2)中猜想的BQ与AP所满足的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由。
(1)AB="AP" ,AB⊥AP ……1’
(2) BQ="AP" ,BQ⊥AP ……2’
延长BQ交AP于点D
 证明△CPQ是等腰直角三角形 ……3’
证明△CPQ是等腰直角三角形 ……3’
则CQ=CP
证明△ACP和△BCQ全等 ……5’
则有BQ=AP
易证∠ADQ=90°,所以BQ⊥AP ……6’
(3)证明方法和评分标准参照(2)……4’
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.(提示:正方形的四条边都相等,四个角都是直角)
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD所在直线的位置关系为______,线段CF、BD的数量关系为______;
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足 条件时,CF⊥BC(点C、F不重合),并说明理由.

-
科目: 来源: 题型:
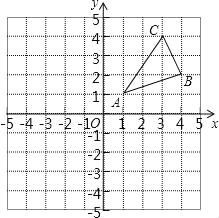
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;
(3)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句:
①一个数的绝对值一定是正数;
②﹣a一定是一个负数;
③没有绝对值为﹣3的数;
④若|a|=a,则a是一个正数;
⑤在原点左边离原点越远的数就越小;
正确的有( )个.
A.0
B.3
C.2
D.4 -
科目: 来源: 题型:
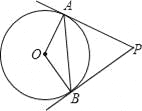
查看答案和解析>>【题目】如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度.
(1)求∠APB的度数;
(2)当OA=3时,求AP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】a是一个两位数,b是一个三位数,把a放在b的右边组成一个五位数,用a,b的代数式表示所得的五位数是( )
A. ba B. 10b+a C. 10000b+a D. 100b+a
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)请在横线上填写合适的内容,完成下面的证明:
如图1,AB∥CD,求证:∠B+∠D=∠BED.
证明:过点E引一条直线EF∥AB
∴∠B=∠BEF,( )
∵AB∥CD,EF∥AB
∴EF∥CD( )
∴∠D=( )
∴∠B+∠D=∠BEF+∠FED
即∠B+∠D=∠BED.
(2)如图2,AB∥CD,请写出∠B+∠BED+∠D=360°的推理过程.
(3)如图3,AB∥CD,请直接写出结果∠B+∠BEF+∠EFD+∠D=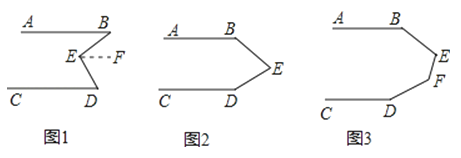
相关试题

