【题目】在第一象限内作射线OC,与x轴的夹角为60°,在射线OC上取一点A,过点A作AH⊥x 轴于点H,在抛物线y=x2(x>0)上取一点P,在y轴上取一点Q,使得以P、O、Q为顶点的三角形与△AOH全等,则符合条件的点A的坐标是______.

参考答案:
【答案】![]()
【解析】试题解析:①如图1,当∠POQ=∠OAH=30°,若以P,O,Q为顶点的三角形与△AOH全等,那么A、P重合;
∵∠AOH=60°,
∴直线OA:y=![]() x,
x,
联立抛物线的解析式得: 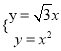 ,
,
解得: ![]() 或
或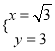 ,
,
故A(![]() ,3);
,3);
②当∠POQ=∠AOH=60°,此时△POQ≌△AOH,
易知∠POH=30°,则直线y=![]() x,联立抛物线的解析式,得:
x,联立抛物线的解析式,得: 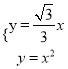 ,
,
解得: ![]() 或
或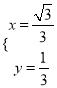 ,
,
故P(![]() ,
, ![]() ),那么A(
),那么A(![]() ,
, ![]() );
);
③当∠OPQ=90°,∠POQ=∠AOH=60°时,此时△QOP≌△AOH;
易知∠POH=30°,则直线y=![]() x,联立抛物线的解析式,得:
x,联立抛物线的解析式,得: 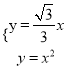 ,
,
解得: ![]() 或
或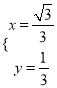 ,
,
故P(![]() ,
, ![]() ),
),
∴OP=![]() ,QP=
,QP=![]() ,
,
∴OH=OP=![]() ,AH=QP=
,AH=QP=![]() ,
,
故A(![]() ,
, ![]() );
);
④当∠OPQ=90°,∠POQ=∠OAH=30°,此时△OQP≌△AOH;
此时直线y=![]() x,联立抛物线的解析式,得:
x,联立抛物线的解析式,得:  ,
,
解得: ![]() 或
或 ,,
,,
∴P(![]() ,3),
,3),
∴QP=2,OP=2![]() ,
,
∴OH=QP=2,AH=OP=2![]() ,
,
故A(2,2![]() ).
).
综上可知:符合条件的点A有四个,分别为:(![]() ,3)或(
,3)或(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() )或(2,2
)或(2,2![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两同学用一副扑克牌中牌面数字分别是3,4,5,6的4张牌做抽数字游戏,游戏规则是:将这4张牌的正面全部朝下,洗匀,从中随机抽取一张,抽得的数作为十位上的数字,抽出的牌不放回,然后将剩下的牌洗匀,再从中随机抽取一张,抽得的数作为个位上的数字,这样就得到一个两位数,若这个两位数小于45,则甲获胜,否则乙获胜.你认为这个游戏公平吗?请利用树状图或列表法说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】深圳某旅行社组织游客到广西桂林旅游,他们要乘船参观桂林山水,若旅行社租用8座的船x艘,则余下6人无座位;若租用12座的船则可少租用1艘,且最后一艘还没坐满,则乘坐最后一艘12座船的人数是( )
A.18﹣4xB.6﹣4xC.30﹣4xD.18﹣8x
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+c与抛物线y=ax2+bx+c的图象都经过y轴上的D点,抛物线与x轴交于A、B两点,其对称轴为直线x=1,且OA=OD.直线y=kx+c与x轴交于点C(点C在点B的右侧).则下列命题中正确命题的是( )
①abc>0; ②3a+b>0; ③﹣1<k<0; ④4a+2b+c<0; ⑤a+b<k.

A. ①②③ B. ②③⑤
C. ②④⑤ D. ②③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x+2与y轴相交于点A0,过点A0作
 轴的平行线交直线y=0.5x+1于点B1,过点 B1作
轴的平行线交直线y=0.5x+1于点B1,过点 B1作 轴的平行线交直线y=x+2于点A1,再过点
轴的平行线交直线y=x+2于点A1,再过点 作
作 轴的平行线交直线y=0.5x+1于点B2,过点 B2作
轴的平行线交直线y=0.5x+1于点B2,过点 B2作 轴的平行线交直线y=x+2于点A2,…,依此类推,得到直线y=x+2上的点A1 ,A2 ,A3 ,…,与直线y=0.5x+1上的点B1,B2,B3,…,则A7B8的长为( )
轴的平行线交直线y=x+2于点A2,…,依此类推,得到直线y=x+2上的点A1 ,A2 ,A3 ,…,与直线y=0.5x+1上的点B1,B2,B3,…,则A7B8的长为( )
A.64 B.128 C.256 D.512
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天,且甲队单独施工45天和乙队单独施工30天的工作量相同.
(1)甲、乙两队单独完成此项任务各需多少天?
(2)若甲、乙两队共同工作了3天后,乙队因设备检修停止施工,由甲队继续施工,为了不影响工程进度,甲队的工作效率提高到原来的2倍,要使甲队总的工作量不少于乙队的工作量的2倍,那么甲队至少再单独施工多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果向东走5m,记作+5m;那么向西走10m,记作______m.
相关试题

