【题目】如图,半圆O的直径AB=10,有一条定长为6的动弦CD在弧AB上滑动(点C、点D分别不与点A、点B重合),点E、F在AB上,EC⊥CD,FD⊥CD. 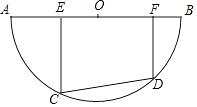
(1)求证:EO=OF;
(2)联结OC,如果△ECO中有一个内角等于45°,求线段EF的长;
(3)当动弦CD在弧AB上滑动时,设变量CE=x,四边形CDFE面积为S,周长为l,问:S与l是否分别随着x的变化而变化?试用所学的函数知识直接写出它们的函数解析式及函数定义域,以说明你的结论.
参考答案:
【答案】
(1)解:证明:过点O作OH⊥CD于H,如图所示:

则CH=DH,
∵EC⊥CD,FD⊥CD,OH⊥CD,
∴EC∥OH∥FD,
∵CH=DH,
∴EO=FO;
(2)解:∵OH⊥CD,OC= ![]() AB=5,
AB=5,
∴CH= ![]() CD=3,
CD=3,
∴OH= ![]() =
= ![]() =4,
=4,
∵EC∥OH,
∴∠ECO=∠COH≠45°;
①当∠EOC=45°时,过点E作EM⊥OC于M,
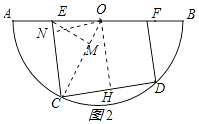
则△OEM是等腰直角三角形,
∴EM=OM,
∵∠ECM=∠COH,∠CME=∠OHC=90°,
∴△ECM∽△COH,
∴EM:CM=CH:OH=3:4.
在Rt△ECM中,设EM=3m,CM=4m.则OM=3m,EO= ![]() OM=3
OM=3 ![]() m,
m,
∵CM+OM=OC,
∴4m+3m=5,
解得:m= ![]() ,
,
∴EO= ![]() ,
,
EF=2EO= ![]() .
.
②当∠CEO=45°时,过点O作ON⊥EC于N;.
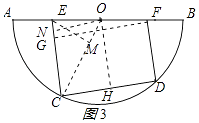
在Rt△CON中,ON=CH=3,CN=OH=4.
在Rt△EON中,EO=3 ![]() .
.
∴EF=2OE=6 ![]() .
.
综上所述,线段EF的长等于 ![]() 或6
或6 ![]()
(3)解:四边形CDFE的面积S不随变量x的变化而变化,是一个不变量;
四边形CDFE的周长l随变量x的变化而变化.理由如下:
由①得:EO=FO,CH=DH,
∴OH是梯形EFDC的中位线,
∴EC+FD=2OH=8,
∴四边形CDFE面积为S= ![]() (EC+FD)CD=OHCD=4×6=24(0<x<8)(是一个常值函数);
(EC+FD)CD=OHCD=4×6=24(0<x<8)(是一个常值函数);
作FG⊥EC于G,则GC=FD=8﹣x,GF=CD=6,
∴EG=EC﹣GC=x﹣(8﹣x)=2x﹣8,
∴EF= ![]() =
= ![]() =2
=2 ![]() ,
,
∴四边形CDFE周长l=EF+EC+CD+FD=EF+2OH+CD=2 ![]() +14(0<x<8),
+14(0<x<8),
即l═2 ![]() +14(0<x<8).
+14(0<x<8).
【解析】(1)过点O作OH⊥CD于H,由垂径定理得出CH=DH,证得EC∥OH∥FD,即可得出结论;(2)由勾股定理求出OH= ![]() ═4,由平行线的性质得出∠ECO=∠COH≠45°;分两种情况讨论:①当∠EOC=45°时,过点E作EM⊥OC于M,则△OEM是等腰直角三角形,得出EM=OM,证明△ECM∽△COH,得出EM:CM=CH:OH=3:4.设EM=3m,CM=4m.则OM=3m,EO=
═4,由平行线的性质得出∠ECO=∠COH≠45°;分两种情况讨论:①当∠EOC=45°时,过点E作EM⊥OC于M,则△OEM是等腰直角三角形,得出EM=OM,证明△ECM∽△COH,得出EM:CM=CH:OH=3:4.设EM=3m,CM=4m.则OM=3m,EO= ![]() OM=3
OM=3 ![]() m,由CM+OM=OC,得出方程4m+3m=5,解方程得出m=
m,由CM+OM=OC,得出方程4m+3m=5,解方程得出m= ![]() ,即可得出EO=
,即可得出EO= ![]() ,EF=2EO=
,EF=2EO= ![]() .②当∠CEO=45°时,过点O作ON⊥EC于N;.在Rt△CON中,ON=CH=3,CN=OH=4.在Rt△EON中,EO=3
.②当∠CEO=45°时,过点O作ON⊥EC于N;.在Rt△CON中,ON=CH=3,CN=OH=4.在Rt△EON中,EO=3 ![]() .得出EF=2OE=6
.得出EF=2OE=6 ![]() 即可.(3)证明OH是梯形EFDC的中位线,由梯形中位线定理得出EC+FD=2OH=8,由梯形面积公式得出S=
即可.(3)证明OH是梯形EFDC的中位线,由梯形中位线定理得出EC+FD=2OH=8,由梯形面积公式得出S= ![]() (EC+FD)CD=OHCD=244×6=24(0<x<8);作FG⊥EC于G,则GC=FD=8﹣x,GF=CD=6,求出EG=EC﹣GC=2x﹣8,由勾股定理得出EF=
(EC+FD)CD=OHCD=244×6=24(0<x<8);作FG⊥EC于G,则GC=FD=8﹣x,GF=CD=6,求出EG=EC﹣GC=2x﹣8,由勾股定理得出EF= ![]() =2
=2 ![]() ,得出四边形CDFE周长l=EF+EC+CD+FD=EF+2OH+CD=2
,得出四边形CDFE周长l=EF+EC+CD+FD=EF+2OH+CD=2 ![]() +14(0<x<8).
+14(0<x<8).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平行四边形ABCD中,AC为对角线,E是边AD上一点,BE⊥AC交AC于点F,BE、CD的延长线交于点G,且∠ABE=∠CAD.

(1)求证:四边形ABCD是矩形;
(2)如果AE=EG,求证:AC2=BCBG. -
科目: 来源: 题型:
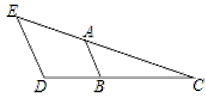
查看答案和解析>>【题目】如图,∠E=50°,∠BAC=50°,∠D=110°,求∠ABD的度数.
请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠E=50°,∠BAC=50°,(已知)
∴∠E= (等量代换)
∴ ∥ .( )
∴∠ABD+∠D=180°.( )
∴∠D=110°,(已知)
∴∠ABD=70°.(等式的性质)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,二次函数y=x2﹣2x+m(m>0)的对称轴与比例系数为5的反比例函数图象交于点A,与x轴交于点B,抛物线的图象与y轴交于点C,且OC=3OB.
(1)求点A的坐标;
(2)求直线AC的表达式;
(3)点E是直线AC上一动点,点F在x轴上方的平面内,且使以A、B、E、F为顶点的四边形是菱形,直接写出点F的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列算式的运算结果为m2的是( )
A.m4m﹣2
B.m6÷m3
C.(m﹣1)2
D.m4﹣m2 -
科目: 来源: 题型:
查看答案和解析>>【题目】李老师用手机软件记录了某个月(30天)每天走路的步数(单位:万步),她将记录的结果绘制成了如图所示的统计图,在李老师每天走路的步数这组数据中,众数与中位数分别为( )

A.1.2与1.3
B.1.4与1.35
C.1.4与1.3
D.1.3与1.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax-2ax-3a(a<0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,抛物线的对称轴与抛物线交于点P,与直线BC交于点M,且PM=
 AB.
AB.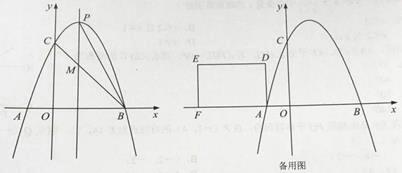
(1)求抛物线的解析式;
(2)点K是x轴正半轴上一点,点A、P关于点K的对称点分别为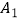 、
、 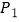 ,连接
,连接 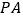 、
、 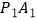 ,若
,若 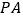
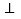
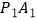 ,求点K的坐标;
,求点K的坐标;
(3)矩形ADEF的边AF在x轴负半轴上,边AD在第二象限,AD=2,DE=3.将矩形ADEF沿x轴正方向平移t(t>0)个单位,直线AD、EF分别交抛物线于G、H.问:是否存在实数t,使得以点D、F、G、H为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,说明理由.
相关试题

