【题目】如图所示的图形中,所有四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形边长为7cm,设正方形A、B、C、D、E、F面积分别为SA、SB、SC、SD、SE、SF,则下列各式正确有()个.
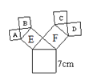
① SA+SB+SC+SD=49;② SE+SF=49;③ SA+SB+SF=49;④ SC+SD+SE=4
A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】D
【解析】
如下图,根据勾股定理得a2+b2=e2、c2+d2=f2、e2+f2=g2,即a2+b2+c2+d2 =g2即可解题.
解:如下图,设正方形的边长分别为a、b、c、d、e、f、g,
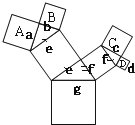
根据正方形的面积公式等于边长的平方,
∴四边形A的面积是a2,四边形B的面积是b2,
a、b是对应直角三角形的直角边,根据勾股定理,则有a2+b2=e2;
同理,四边形C的面积是c2,四边形D的面积是d2,
c、d是对应直角三角形的直角边,根据勾股定理,则有c2+d2=f2;
根据正方形的对边相等,e、f就是下面大直角三角形的直角边,根据勾股定理,得到e2+f2=g2,
∵g是最大的正方形边长为7cm,
∴正方形A、B、C、D面积之和为7×7=49平方厘米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某校学生对以下四个电视节目:
 最强大脑
最强大脑 、
、 中国诗词大会
中国诗词大会 、
、 朗读者
朗读者 、
、 出彩中国人
出彩中国人 的喜爱情况,随机抽取了部分学生进行调查,要求每名学生选出并且只能选出一个自己最喜爱的节目,根据调查结果,绘制了如下两幅不完整的统计图.
的喜爱情况,随机抽取了部分学生进行调查,要求每名学生选出并且只能选出一个自己最喜爱的节目,根据调查结果,绘制了如下两幅不完整的统计图.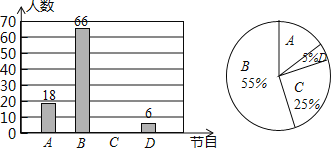
请你根据图中所提供的信息,完成下列问题:
 本次调查的学生人数为______;
本次调查的学生人数为______; 在扇形统计图中,A部分所占圆心角的度数为______;
在扇形统计图中,A部分所占圆心角的度数为______;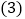 请将条形统计图补充完整;
请将条形统计图补充完整;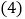 若该校共有3000名学生,估计该校最喜爱
若该校共有3000名学生,估计该校最喜爱 中国诗词大会
中国诗词大会 的学生有多少名.
的学生有多少名. -
科目: 来源: 题型:
查看答案和解析>>【题目】超市准备购进A、B两种品牌的饮料共100件,两种饮料每件利润分别是15元和13元.设购进A种饮料x件,且所购进的两种饮料能全部卖出,获得的总利润为y元.
(1)求y与x的函数关系式;
(2)根据两种饮料历次销量记载:A种饮料至少购进30件,B种饮料购进数量不少于A种饮料件数的2倍.问:A、B两种饮料进货方案有几种?哪一种方案能使超市所获利润最高?最高利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆柱底面半径为
 cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )A. 12cm B.
 cm C. 15cm D.
cm C. 15cm D.  cm
cm -
科目: 来源: 题型:
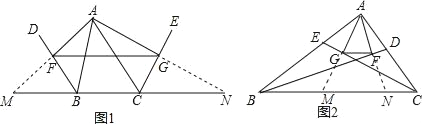
查看答案和解析>>【题目】几何证明:
(1)已知:如图1,BD、CE分别是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别是F、G,连接FG,延长AF、AG,与直线BC相交.求证:FG=
 (AB+BC+AC).
(AB+BC+AC).(2)若BD、CE分别是△ABC的内角平分线,其余条件不变(如图1),线段FG与△ABC的三边又有怎样的数量关系?写出你的猜想,并给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天)
1≤x<50
50≤x≤90
售价(元/件)
x+40
90
每天销量(件)
200﹣2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】为顺利通过“国家文明城市”验收,东营市政府拟对城区部分路段的人行道地砖、绿化带、排水管道等公用设施全面更新改造,根据市政建设的需要,需在40天内完成工程.现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作只需10天完成.
(1)甲、乙两个工程队单独完成此项工程各需多少天?
(2)若甲工程队每天的工程费用是4.5万元,乙工程队每天的工程费用是2.5万元,请你设计一种方案,既能按时完工,又能使工程费用最少.
相关试题

