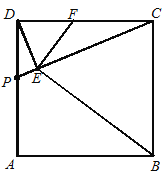
【题目】如图,正方形ABCD中,点P是AD上的一动点(与点D、点A不重合),DE⊥CP,垂足为E,EF⊥BE与DC交于点F.
(1)求证:△DEF∽△CEB;
(2)当点P运动到DA的中点时,求证:点F为DC的中点.
参考答案:
【答案】证明见解析
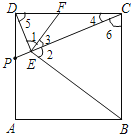
【解析】试题分析:(1)由DE⊥CP,EF⊥BE,则∠1+∠3=∠DEC=90°,∠2+∠3=∠FEB=90°,根据等角的余角相等得∠1=∠2,再根据正方形的性质得∠4+∠6=90°,而∠4+∠5=90°,则∠5=∠6,根据相似三角形的判定即可得到结论;
(2)根据正方形的性质得AD=DC=BC,而点P为DA的中点,则PD=![]() AD=
AD=![]() DC,再根据正切的定义得到tan∠4=
DC,再根据正切的定义得到tan∠4=![]() ,tan∠4=
,tan∠4=![]() ,则
,则![]() ,然后根据△DEF∽△CEB得到
,然后根据△DEF∽△CEB得到![]() ,易得
,易得![]() ,即可得到结论.
,即可得到结论.
试题解析:(1)∵DE⊥CP,EF⊥BE,
∴∠1+∠3=∠DEC=90°,∠2+∠3=∠FEB=90°,
∴∠1=∠2,
∵四边形ABCD是正方形,
∴∠4+∠6=∠DCB=90°,
而在Rt△DEC中,∠4+∠5=90°,
∴∠5=∠6,
∴△DEF∽△CEB;
(2)∵四边形ABCD是正方形,
∴AD=DC=BC,
∵点P为DA的中点,
∴PD=![]() AD=
AD=![]() DC,
DC,
在Rt△PDC中,tan∠4=![]() ,
,
在Rt△DEC中,tan∠4=![]() ,
,
∴![]() ,
,
∵△DEF∽△CEB,
∴![]() ,
,
而CB=DC,
∴![]() ,
,
∴点F为DC的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】袋子中装有2个红球,1个黄球,它们除颜色外其余都相同. 小明和小张做摸球游戏,约定一次游戏规则是:小张先从袋中任意摸出1个球记下颜色后放回,小明再从袋中摸出1个球记下颜色后放回,如果两人摸到的球的颜色相同,小张赢,否则小明赢.
(1)请用树状图或列表格法表示一次游戏中所有可能出现的结果;
(2)这个游戏规则对双方公平吗?请说明理由.
-
科目: 来源: 题型:
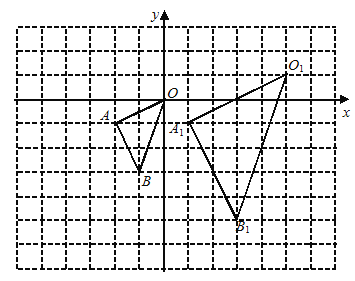
查看答案和解析>>【题目】在下图的方格纸中,△OAB的顶点坐标分别为O(0,0)、A(-2,-1)、B(-1,-3),△O1A1B1与△OAB是关于点P为位似中心的位似图形.
(1)在图中标出位似中心P的位置,并写出点P及点B的对应点B1的坐标;
(2)以原点O为位似中心,在位似中心的同侧画出△OAB的一个位似△OA2B2,使它与△OAB的相似比为2:1. 并写出点B的对应点B2的坐标;
(3)△OAB 内部一点M的坐标为(a,b),写出M在△OA2B2中的对应点M2的坐标;
(4)判断△OA2B2能否看作是由△O1A1B1经过某种变换后得到的图形,若是,请指出是怎样变换得到的(直接写答案).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知△ABC中,∠B=90°,AB=16cm,AC=20cm,P、Q是△ABC的边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为ts.
(1)则BC= cm;
(2)当t为何值时,点P在边AC的垂直平分线上?此时CQ= ;
(3)当点Q在边CA上运动时,直接写出使△BCQ成为等腰三角形的运动时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】⊙O的半径为5cm,AB,CD是⊙O的两条弦,AB‖CD,AB=8,CD=6,AB和CD之间的距离是___________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,已知点A(﹣3,0)、B(0,4),对△OAB连续作翻转变换,依次得到△1、△2、△3、△4…,则△23中的
 的坐标为_______________。
的坐标为_______________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某旅行团上午6时从旅馆出发,乘汽车到距离210km的著名旅游景点游玩,已知该汽车离旅馆的距离S(km)与时间t(h)的关系如图所示,根据图像提供的信息,解答以下问题:

(1)求该旅行团在景点游玩了多少小时?
(2)求该旅行团去景点的平均速度?
(3)求返回宾馆时该汽车离旅馆的距离S(km)与时间t(h)的关系式.
相关试题

