[题目]对于非零实数a.b.规定ab＝.若(x﹣3)(3﹣2x)＝0.则x的值为 ,若关于x的方程(x﹣3)(3﹣2x)﹣(3﹣x)(mx﹣2)＝﹣1无解.则m的值为．题目和参考答案 ——青夏教育精英家教网—

【题目】对于非零实数a、b，规定ab＝，若（x﹣3）（3﹣2x）＝0，则x的值为_____；若关于x的方程（x﹣3）（3﹣2x）﹣（3﹣x）（mx﹣2）＝﹣1无解，则m的值为_____．

参考答案：

【答案】或1.

【解析】

已知等式利用题中的新定义化简，计算即可求出x的值；已知等式利用题中的新定义化简，根据分式方程无解分情况求出m的值即可．

解：已知等式利用题中的新定义化简得：＝0，

解得：x＝，

经检验x＝是分式方程的解，

则x的值为；

已知等式利用题中的新定义化简得：﹣＝﹣1，

去分母得：3﹣2x+mx﹣2＝3﹣x，整理得：（m-1）x-2=0，

①由分式方程有增根，得到x﹣3＝0，即x＝3，

把x＝3代入整式方程得：3m﹣3﹣2＝0，

解得：m＝，

②整式方程无解，则m-1＝0，

解得m=1，

故答案为：；或1.

相关试题

科目： 来源： 题型：

【题目】定义：如图1，在△ABC和△ADE中，AB=AC=AD=AE，当∠BAC+∠DAE=180°时，我们称△ABC与△DAE互为“顶补等腰三角形”，△ABC的边BC上的高线AM叫做△ADE的“顶心距”，点A叫做“旋补中心”．
特例感知：
（1）在图2，图3中，△ABC与△DAE互为“顶补三角形”，AM，AN是“顶心距”．
①如图2，当∠BAC=90°时，AM与DE之间的数量关系为AM=　　DE；
②如图3，当∠BAC=120°，BC=6时，AN的长为　　．
猜想论证：
（2）在图1中，当∠BAC为任意角时，猜想AM与DE之间的数量关系，并给予证明．
拓展应用
（3）如图4，在四边形ABCD，AD=AB，CD=BC，∠B=90°，∠A=60°，CD=2，在四边形ABCD的内部是否存在点P，使得△PAD与△PBC互为“顶补等腰三角形”？若存在，请给予证明，并求△PBC的“顶心距”的长；若不存在，请说明理由．
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，AB＝BC，AB⊥BC，过点B作直线l，过点A作AE⊥l于E，过点C作CF⊥l于F，则下列说法中正确的是（　　）
A.AC＝AE+BEB.EF＝AE+EBC.AC＝EB+CFD.EF＝EB+CF
查看答案和解析>>
科目： 来源： 题型：

【题目】下列命题中：
①已知两实数a、b，如果a＞b，那么a2＞b2；②同位角相等，两直线平行；③如果两个角是直角，那么这两个角相等；④如果分式无意义，那么x＝﹣；这些命题及其逆命题都是真命题的是（　　）
A.①②B.③④C.①③D.②④
查看答案和解析>>
科目： 来源： 题型：

【题目】综合与探究
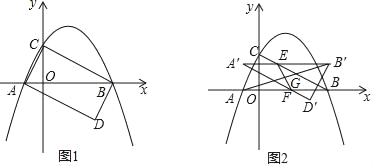
如图1，抛物线y=ax2+bx+2与x轴交于A（﹣1，0），B（4，0）两点，与y轴交于点C，连接AC，BC．D为坐标平面第四象限内一点，且使得△ABD与△ABC全等．
（1）求抛物线的表达式．
（2）请直接写出点D的坐标，并判断四边形ACBD的形状．
（3）如图2，将△ABD沿y轴的正方形以每秒1个单位长度的速度平移，得到△A′B′D′，A′B′与BC交于点E，A′D′与AB交于点F．连接EF，AB′，EF与AB′交于点G．设运动的时间为t（0≤t≤2）秒．
①当直线EF经过抛物线的顶点T时，请求出此时t的值；
②请直接写出点G经过的路径的长．
查看答案和解析>>
科目： 来源： 题型：

【题目】在平面直角坐标系xOy中，将一块含有45°角的直角三角板如图放置，直角顶点C的坐标为（1，0），顶点A的坐标为（0，2），顶点B恰好落在第一象限的双曲线上，现将直角三角板沿x轴正方向平移，当顶点A恰好落在该双曲线上时停止运动，则此时点C的对应点C′的坐标为（　　）
A. （，0） B. （2，0） C. （，0） D. （3，0）
查看答案和解析>>
科目： 来源： 题型：

【题目】已知，在△ABC中，∠ACB＝90°，AC＝BC，D为直线AB上一点，作直线CD，AE⊥CD于E，BF⊥CD于F．
（1）若D在线段AB上，如图，试猜想线段EF、AE和BF之间的数量关系，并证明你的猜想；
（2）若D在线段AB的延长线上，请你根据题意画出图形，试猜想线段EF、AE和BF之间的数量关系，并证明你的猜想．
查看答案和解析>>