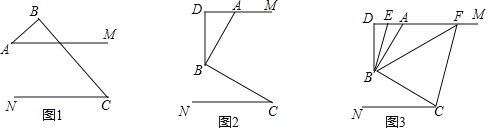
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,直接写出∠A和∠C之间的数量关系________;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
参考答案:
【答案】(1)∠A+∠C=90°;(2)见解析;(3)105°.
【解析】试题分析:(1)根据平行线的性质以及直角三角形的性质进行证明即可; (2)先过点B作BG∥DM,根据同角的余角相等,得出∠ABD=∠CBG,再根据平行线的性质,得出∠C=∠CBG,即可得结论;(3)先过点B作BG∥DM,根据角平分线的定义,得出∠ABF=∠GBF,设∠DBE=α,∠ABF=β,根据由∠CBF+∠BFC+∠BCF=180°,可得(2α+β)+3α+(3α+β)=180°,根据AB⊥BC,可得β+β+2α=90°,最后解方程组即可得到∠ABE=15°,进而得∠EBC=∠ABE+∠ABC=15°+90°=105°.
试题解析:
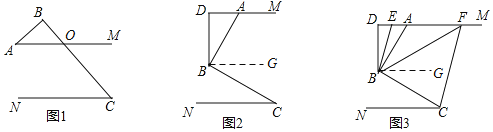
(1)如图1,∵AM∥CN,
∴∠C=∠AOB,
∵AB⊥BC,
∴∠A+∠AOB=90°,
∴∠A+∠C=90°,
(2)如图2,过点B作BG∥DM,
∵BD⊥AM,
∴DB⊥BG,即∠ABD+∠ABG=90°,
又∵AB⊥BC,
∴∠CBG+∠ABG=90°,
∴∠ABD=∠CBG,
∵AM∥CN,
∴∠C=∠CBG,
∴∠ABD=∠C;
(3)如图3,过点B作BG∥DM,
∵BF平分∠DBC,BE平分∠ABD,
∴∠DBF=∠CBF,∠DBE=∠ABE,
由(2)可得∠ABD=∠CBG,
∴∠ABF=∠GBF,
设∠DBE=α,∠ABF=β,则
∠ABE=α,∠ABD=2α=∠CBG,∠GBF=β=∠AFB,∠BFC=3∠DBE=3α,
∴∠AFC=3α+β,
∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,
∴∠FCB=∠AFC=3α+β,
△BCF中,由∠CBF+∠BFC+∠BCF=180°,可得
(2α+β)+3α+(3α+β)=180°,①
由AB⊥BC,可得
β+β+2α=90°,②
由①②联立方程组,解得α=15°,
∴∠ABE=15°,
∴∠EBC=∠ABE+∠ABC=15°+90°=105°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值.2(x﹣3)(x+2)﹣(3+a)(﹣a+3),其中,a=﹣2,x=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知﹣1<y<3,化简|y+1|+|y﹣3|=( )
A. 4 B. -4 C. 2y-2 D. -2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元,售出3件A种商品和5件B种商品所得利润为1100元;
(1)求每件A种商品和每件B种商品售出后所得利润各多少元?
(2)若该商场一次购进A、B两种商品共34件,全部售完后所得利润不低于4000元,那么该商场至少需要购进多少件A种商品?
-
科目: 来源: 题型:
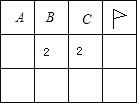
查看答案和解析>>【题目】Windows2000下有一个有趣的游戏“扫雷”,下图是扫雷游戏的一部分:(说明:图中数字2表示在以该数字为中心的8个方格中有2个地雷).小旗表示该方格已被探明有地雷,现在还剩下A、B、C三个方格未被探明,其它地方为安全区(包括有数字的方格)
(1)现在还剩下几个地雷?
(2)A、B、C三个方格中有地雷的概率分别是多大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形不一定具有的性质是( )
A.对角线互相垂直B.对边平行且相等C.对角线互相平分D.对角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】小夏为了了解她所在小区(约有3000人)市民的运动健身情况,她应采用的收集数据的方式是( )
A. 对小区所有成年人发问卷调查
B. 对小区内所有中小学生发问卷调查
C. 在小区出入居民随机发问卷进行调查
D. 挨家挨户发问卷调查
相关试题

