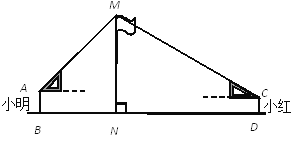
【题目】如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).求出旗杆MN的高度.(参考数据: ![]() ,结果保留整数.)
,结果保留整数.)
参考答案:
【答案】旗杆高约为12米.
【解析】试题分析:过点A作AE⊥MN于E,过点C作CF⊥MN于F,则EF=0.2m.由△AEM是等腰直角三角形得出AE=ME,设AE=ME=xm,则MF=(x+0.2)m,FC=(28-x)m.在Rt△MFC中,由MF=CFtan∠MCF,解方程求出x的值,则MN=ME+EN.
试题解析: 过点A作AE⊥MN于E,
过点C作CF⊥MN于F
则EF= ![]() =0.2
=0.2
在Rt△AEM中,
∵∠MAE=45°,∴AE=ME
设AE=ME= ![]() (不设参数也可)
(不设参数也可)
∴MF= ![]() +0.2,CF=28
+0.2,CF=28 ![]()
在Rt△MFC中,∠MFC=90°,∠MCF=30°
∴MF=CF·tan∠MCF
∴![]()
∴![]() 10.0
10.0
∴MN![]() 12
12
答:旗杆高约为12米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角α(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
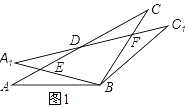
(1)如图1,观察并猜想,在旋转过程中,线段BE与BF有怎样的数量关系?并证明你的结论;
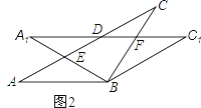
(2)如图2,当α=30°时,试判断四边形BC1DA的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“QQ空间”等级是用户资料和身份的象征,按照空间积分划分不同的等级.当用户在10级以上,每个等级与对应的积分有一定的关系.现在知道第10级的积分是90,第11级的积分是160,第12级的积分是250,第13级的积分是360,第14级的积分是490…若某用户的空间积分达到1000,则他的等级是( )
A.15B.16C.17D.18
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知P是⊙O外一点,PO交⊙O于点C,OC=CP=2,弦AB⊥OC,∠AOC的度数为60°,连接PB.
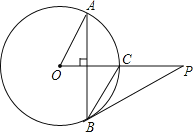
(1)求BC的长;
(2)求证:PB是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“囧”
 是近时期网络流行语,像一个人脸郁闷的神情
是近时期网络流行语,像一个人脸郁闷的神情 如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案
如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案 阴影部分
阴影部分 设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.
设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.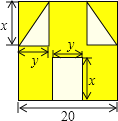
(1)用含有x、y的代数式表示下图中“囧”的面积;
(2)当
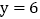 ,
,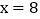 时,求此时“囧”的面积.
时,求此时“囧”的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】补全解题过程.
已知:如图,O是直线AB上的一点,∠COD=90°,OE平分∠BOC.若∠AOC=60°,求∠DOE数.
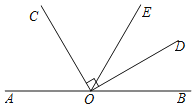
解:∵O是直线AB上的一点,(已知)
∴∠BOC=180°﹣∠AOC.(_________)
∵∠AOC=60°,(已知)
∴∠BOC=120°.(_________)
∵OE平分∠BOC,(已知)
∴∠COE=
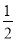 ∠BOC,(_________)
∠BOC,(_________)∴∠COE=_____°.
∵∠DOE=∠COD﹣∠COE,且∠COD=90°,
∴∠DOE=_____°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(注:结果保留π )
(1)把圆片沿数轴向右滚动半周,点B到达数轴上点C的位置,点C表示的数是 数(填“无理”或“有理”),这个数是 ;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是 ;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3.
①第 次滚动后,A点距离原点最近,第 次滚动后,A点距离原点最远.
②当圆片结束运动时,A点运动的路程共有 ,此时点A所表示的数是 .

相关试题

