【题目】今年年初,我国爆发新冠肺炎疫情,某省邻近县市 C、D 获知 A、B 两市分别急需救援物资 200吨和 300 吨的消息后,决定调运物资支援.已知 C 市有救援物资 240 吨,D 市有救援物资 260 吨,现将这些救援物资全部调往 A、B 两市.已知从 C 市运往 A、B 两市的费用分别为每吨 20 元和 25 元,从D 市运往往 A、B 两市的费用分别为每吨 15 元和 30 元,设从 C 市运往 A 市的救援物资为 x 吨.
(1) 请填写下表;
A | B | 合计(吨) | |
C | x | _____ | 240 |
D | _____ | _____ | 260 |
总计(吨) | 200 | 300 | 500 |
(2)设 C、D 两市的总运费为 W 元,则 W 与 x 之间的函数关系式为_________,其中自变量 x的取值范围是________;
(3)经过抢修,从 C 市到 B 市的路况得到了改善,缩短了运输时间,运费每吨减少 n 元(n>10),其余路线运费不变,若 C、D 两市的总运费的最小值不小于 7920 元,则 n 的取值范围是______________.
参考答案:
【答案】![]()
![]()
![]()
![]()
![]()
![]()
【解析】
(1)根据题意可以将表格中的空缺数据补充完整;
(2)根据题意可以求得W与x的函数关系式,并写出x的取值范围;
(3)根据题意可得![]() ,再根据x的取值范围解不等式即可求解n 的取值范围.
,再根据x的取值范围解不等式即可求解n 的取值范围.
(1)∵从 C 市运往 A 市的救援物资为 x 吨
∴从 C 市运往 B 市的救援物资为![]() 吨,从 D 市运往 A 市的救援物资为
吨,从 D 市运往 A 市的救援物资为 ![]() 吨,从 D 市运往 B 市的救援物资为
吨,从 D 市运往 B 市的救援物资为![]() 吨
吨
故答案为:![]() ,
,![]() ,
,![]() ;
;
(2)由题意可得
![]()
![]()
![]()
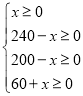
解得![]() ;
;
(3)由题意可得
![]()
![]()
![]()
∵![]()
∴![]()
∵C、D 两市的总运费的最小值不小于 7920 元
∴![]()
![]()
![]()
∵![]()
∴![]()
![]()
![]()
∵![]()
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个盒子里有标号分别为1,2,3,4,5,6的六个小球,这些小球除标号数字外都相同.
(1)从盒中随机摸出一个小球,求摸到标号数字为奇数的小球的概率;
(2)甲、乙两人用这六个小球玩摸球游戏,规则是:甲从盒中随机摸出一个小球,记下标号数字后放回盒里,充分摇匀后,乙再从盒中随机摸出一个小球,并记下标号数字.若两次摸到小球的标号数字同为奇数或同为偶数,则判甲赢;若两次摸到小球的标号数字为一奇一偶,则判乙赢.请用列表法或画树状图的方法说明这个游戏对甲、乙两人是否公平. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的方格纸中,小正方形的顶点叫做格点,
 是一个格点三角形(即
是一个格点三角形(即 的三个顶点都在格点上),根据要求回答下列问题:
的三个顶点都在格点上),根据要求回答下列问题:
(1)画出
 先向右平移6格,再向下平移2格所得的
先向右平移6格,再向下平移2格所得的 ;
;(2)过点B画直线
 ,将
,将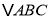 分成面积相等的两个三角形;
分成面积相等的两个三角形;(3)
 的面积是 ;
的面积是 ; -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线 AB与 x 轴,y 轴分别交于点 A和点 B,点 A的坐标为(1,0),且 2OA=OB.
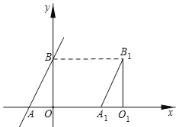
(1)求直线 AB 解析式;
(2)如图,将△A O B 向右平移 3 个单位长度,得到△A1O1B1,求线段 O B1的长;
(3)在(2)中△AOB 扫过的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地而上向建筑物前进了50m到达D处,此时遇到一斜坡,坡度i=1:
 ,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1:
,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1: 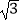 是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取
是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取 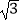 =1.732,结果精确到0.1m).
=1.732,结果精确到0.1m).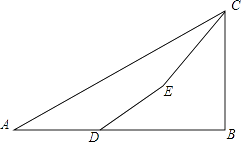
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AE、BF是角平分线,它们相交于点O,AD是高,∠BAC=50°,∠C=70°,求∠DAE,∠AOB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O是坐标原点,ABCD的顶点A的坐标为(﹣2,0),点D的坐标为(0,2
 ),点B在x轴的正半轴上,点E为线段AD的中点
),点B在x轴的正半轴上,点E为线段AD的中点
(1)如图1,求∠DAO的大小及线段DE的长;
(2)过点E的直线l与x轴交于点F,与射线DC交于点G.连接OE,△OEF′是△OEF关于直线OE对称的图形,记直线EF′与射线DC的交点为H,△EHC的面积为3 .
.
①如图2,当点G在点H的左侧时,求GH,DG的长;
②当点G在点H的右侧时,求点F的坐标(直接写出结果即可).
相关试题

