【题目】如图,将边长为1cm的等边三角形ABC沿直线l向右翻动(不滑动),点B从开始到结束,所经过路径的长度为( ) 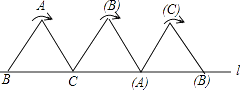
A.![]() cm
cm
B.(2+ ![]() π)cm
π)cm
C.![]() cm
cm
D.3cm
参考答案:
【答案】C
【解析】解:∵△ABC是等边三角形, ∴∠ACB=60°,
∴∠AC(A)=120°,
点B两次翻动划过的弧长相等,
则点B经过的路径长=2× ![]() =
= ![]() π.
π.
故选C.
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°,以及对弧长计算公式的理解,了解若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),P6(2,0),…,则点P2017的坐标是( )
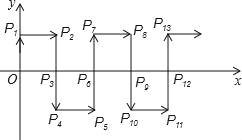
A. (671,﹣1) B. (672,0) C. (672,1) D. (672,﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1∥l2 , 若∠1=140°,∠2=70°,则∠3的度数是( )
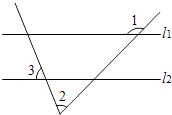
A.70°
B.80°
C.65°
D.60° -
科目: 来源: 题型:
查看答案和解析>>【题目】“校园手机”现象越来越受到社会的关注.“寒假”期间,某校小记者随机调查了某地区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图:

(1)求这次调查的家长人数,并补全图1;
(2)求图2中表示家长“赞成”的圆心角的度数;
(3)已知某地区共6500名家长,估计其中反对中学生带手机的大约有多少名家长?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.试判断四边形ADCF的形状,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,三角形ABC三个顶点A,B,C的坐标分别为A(1,2),B(4,3),C(3,1).
(1)三角形A1B1C1向右平移4个单位长度,再向下平移3个单位长度,恰好得到三角形ABC,试写出三角形A1B1C1三个顶点的坐标.
(2)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
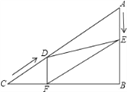
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
相关试题

