【题目】某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16nmile,“海天”号每小时航行12nmile,它们离开港口一个半小时后相距30nmile,且知道“远航”号沿东北方向航行,那么“海天”号航行的方向是 .
参考答案:
【答案】西北方向
【解析】解:根据题意,得 PQ=16×1.5=24(海里),PR=12×1.5=18(海里),QR=30(海里).
∵242+182=302 ,
即PQ2+PR2=QR2 ,
∴∠QPR=90°.
由“远航号”沿东北方向航行可知,∠QPS=45°,则∠SPR=45°,即“海天”号沿西北方向航行.
故答案是:西北方向.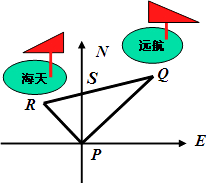
根据路程=速度×时间分别求得PQ、PR的长,再进一步根据勾股定理的逆定理可以证明三角形PQR是直角三角形,从而求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用平移、旋转和对称变换可以设计出美丽的镶嵌图案;这种说法_____________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线
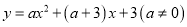 与
与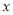 轴交于点A(4,0),与
轴交于点A(4,0),与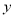 轴交于点B,在x轴上有一动点E(m,0)(0<m<4),过点E作
轴交于点B,在x轴上有一动点E(m,0)(0<m<4),过点E作 轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.(1)求
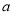 的值和直线AB的函数表达式;
的值和直线AB的函数表达式;(2)在P点运动的过程中,请用含m的代数式表示线段PN;
(3)设△PMN的周长为
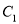 ,△AEN的周长为
,△AEN的周长为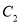 ,若
,若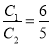 ,求m的值;
,求m的值;(4)如图2,在(3)条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<90°),连接
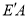 、
、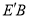 ,求
,求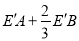 的最小值.
的最小值.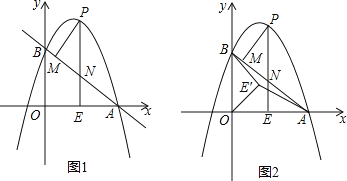
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(x﹣2)(﹣x﹣2)=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若4x2+kx+25=(2x-5)2,那么k的值是
-
科目: 来源: 题型:
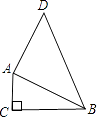
查看答案和解析>>【题目】如图,∠C=90°,AC=3,BC=4,AD=12,BD=13,试判断△ABD的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国际奥委会会旗上的五环图案可以看作一个基本图案圆环经过______运动得到
相关试题

