【题目】如图,在△ABC中,AC=BC,∠ ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DF⊥AC交AC的延长线于F,连接CD,给出四个结论:①∠ADC=45°;②BD=![]() AE;③AC+CE=AB;④AB—BC=2FC;其中正确的结论有( )
AE;③AC+CE=AB;④AB—BC=2FC;其中正确的结论有( )
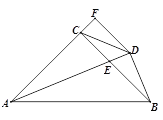
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】D
【解析】试题分析:过点E作EQ⊥AB于Q,∵∠ACB=90°,AE平分∠CAB,∴CE=EQ,∵∠ACB=90°,AC=BC ∴∠CBA=∠CAB=45° ∵EQ⊥AB ∴∠EQA=∠EQB=90° 由勾股定理可得AC=AQ ∴∠QEB=45°=∠CBA
∴EQ=BQ ∴AB=AQ+BQ=AC+CE ∴③正确
作∠ACN=∠BCD,交AD于N,∵∠CAD=![]() ∠CAB=22.5°=∠BAD ∴∠ABD=67.5° ∴∠DBC=22.5°=∠CAD
∠CAB=22.5°=∠BAD ∴∠ABD=67.5° ∴∠DBC=22.5°=∠CAD
∴∠DBC=∠CAD ∵AC=BC ∠ACN=∠DCB ∴△ACN≌△BCD ∴CN=CD AN=BD ∵∠ACN+∠NCE=90°
∴∠NCB+∠BCD=90° ∴∠CND=∠CDA=45° ∴∠ACN=22.5°=∠CAN ∴AN=CN ∴∠NCE=∠AEC=67.5°
∴CN=NE ∴CD-AN=EN=![]() AE ∵AN=BD ∴BD=
AE ∵AN=BD ∴BD=![]() AE ∴①正确 ②正确.
AE ∴①正确 ②正确.
过D作DH⊥AB于H,∵∠FCD=∠CAD+∠CDA=67.5° ∠DBA=90°-∠DAB=67.5° ∴∠FCD=∠DBA
∵AE平分∠CAB DF⊥AC,DH⊥AB,∴DF=DH ∴△DCF≌△DBH ∴BH=CF 由勾股定理可得:AF=AH
∴![]() ,∴AC+AB=2AF AC+AB=2AC+2CF
,∴AC+AB=2AF AC+AB=2AC+2CF
AB-AC=2CF ∵AC=CB ∴AB-CB=2CF ∴④正确.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在y=5x+a-2中,若y是x的正比例函数,则常数a=
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果A=5x2+4x﹣1,B=﹣x2﹣3x﹣3,C=8﹣7x﹣6x2 , 小聪在计算A﹣B+C的值后判断A﹣B+C的值与x无关,请你说明小聪的判断是否正确,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形的两边长分别为3和6,第三边的长是方程x2-6x+8=0的一个根,则这个三角形的周长是( )
A. 9 B. 11 C. 13 D. 11或13
-
科目: 来源: 题型:
查看答案和解析>>【题目】① 如图,由小正方形组成的L形图中,用三种方法分别在图中添一个小正方形使图形成为轴对称图形:
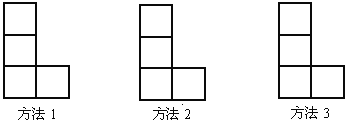
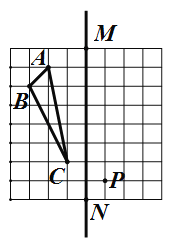
② 如图,在正方形网格上的一个△ABC.
⑴ 作△ABC关于直线MN的对称图形(不写作法);
⑵ 以P为一个顶点作与△ABC全等的三角形(规定点P与点B对应,另两顶点都在图中网格交点处),则可作出 个三角形与△ABC全等.
-
科目: 来源: 题型:
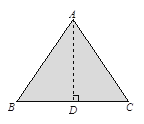
查看答案和解析>>【题目】操作探究:(1)现有一块等腰三角形纸板,量得周长为32cm,底比一腰多2cm.若把这个三角形纸板沿其对称轴剪开,拼成一个四边形,请画出你能拼成的各种四边形的示意图
(2)计算拼成的各个四边形的两条对角线长的平方和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个城镇A、B与两条公路l1、l2位置如图所示,电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路l1,l2的距离也必须相等,那么点C应选在何处?请在图中,用尺规作图找出所有符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)

相关试题

