【题目】如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴,
轴,![]() 轴交于
轴交于![]() 两点.
两点.
(1)求线段AB的长度;
(2)若点![]() 在第二象限,且△
在第二象限,且△![]() 为等腰直角三角形,求点
为等腰直角三角形,求点![]() 的坐标;
的坐标;

参考答案:
【答案】(1)5(2)(-3,7)(-7,4)(-![]() ,
,![]() )
)
【解析】
(1)先求出A,B的坐标,根据勾股定理,得到AB的长;
(2)分三种情况分别进行讨论.
解:(1)当x=0,得y=3,
当y=0,x=-4,
∴A(-4,0),B(0,3),即OA=4,OB=3,
∴根据勾股定理AB=5;
(2)①过点A作C1A⊥AB,截取AC1=AB,此时△AC1B是等腰直角三角形,

过C1作C1D1⊥x轴于D1,此时Rt△C1D1A≌Rt△AOB,
∴C1D1=OA=4,AD1=OB=3,OD1=7,
∴C1(-7,4);
②过点B作C2B⊥AB,截取BC2=AB,此时△AC2B是等腰直角三角形,

过C2作C2D2⊥y轴于D2,此时Rt△C2D2B≌Rt△BOA,
∴C2D2=OB=3,BD2=OA=4,OD2=7,
∴C2(-3,7);
③以AB为腰,作等腰直角△AC3B,
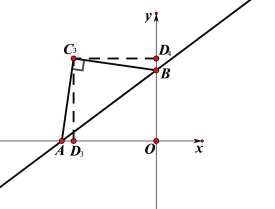
过C3作C3D3⊥OA,作C3D4⊥OB,此时Rt△C3D3A≌Rt△C3D4B,四边形C3D3OD4是正方形,
∴AD3=BD4,
∴OA-AD3=OB+BD4,即4-AD3=3+BD4,
∴AD3=BD4=![]() ,
,
∴OD3=4-![]() ,OD4=3+
,OD4=3+![]() =
=![]() ,
,
∴C3(-![]() ,
,![]() ).
).
故答案为:(1)5;(2)(-3,7)(-7,4)(-![]() ,
,![]() )
)
-
科目: 来源: 题型:
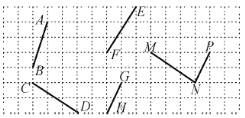
查看答案和解析>>【题目】如图,在下面的方格纸中,找出互相平行的线段,并用符号表示出来:__________,__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形ABC的三条内角平分线为AE、BF、CG,下面的说法中正确的个数有( )
①△ABC的内角平分线上的点到三边距离相等
②三角形的三条内角平分线交于一点
③三角形的内角平分线位于三角形的内部
④三角形的任一内角平分线将三角形分成面积相等的两部分.
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
(1)求证:AC=AE;
(2)若点E为AB的中点,CD=4,求BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于三个数
 ,用
,用 表示这三个数中最大数,例如:
表示这三个数中最大数,例如: ,
,
解决问题:
(1)填空:
 {
{ ,
, ,
, }= ,如果
}= ,如果 {
{ ,
, ,
, }=
}= ,则
,则 的取值范围为 ;
的取值范围为 ;(2)如果
 {
{ ,
, ,
, }=
}= ,求
,求 的值;
的值;(3)如图,在同一坐标系中画出了三个一次函数的图象:
 ,
, 和
和

请观察这三个函数的图象,
①在图中画出
 {
{ ,
, ,
, }对应的图像(加粗);
}对应的图像(加粗);②
 {
{ ,
, ,
, }的最小值为 .
}的最小值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】基本图形:在Rt△
 中,
中, ,
, 为
为 边上一点(不与点
边上一点(不与点 ,
,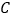 重合),将线段
重合),将线段 绕点
绕点 逆时针旋转
逆时针旋转 得到
得到 .
.探索:(1)连接
 ,如图①,试探索线段
,如图①,试探索线段 之间满足的等量关系,并证明结论;
之间满足的等量关系,并证明结论;(2)连接
 ,如图②,试探索线段
,如图②,试探索线段 之间满足的等量关系,并证明结论;
之间满足的等量关系,并证明结论; 
联想:(3)如图③,在四边形
 中,
中, .若
.若 ,
,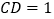 ,则
,则 的长为 .
的长为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:

(1)△AEF≌△CEB;
(2)AF=2CD.
相关试题

