【题目】如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2 , 两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为m. 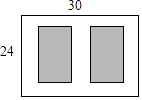
参考答案:
【答案】2
【解析】解:设人行通道的宽度为x米,将两块矩形绿地合在一起长为(30﹣3x)m,宽为(24﹣2x)m, 由已知得:(30﹣3x)(24﹣2x)=480,
整理得:x2﹣22x+40=0,
解得:x1=2,x2=20,
当x=20时,30﹣3x=﹣30,24﹣2x=﹣16,不符合题意舍去,
即x=2.
答:人行通道的宽度为2米.
故答案为2.
设人行通道的宽度为x米,将两块矩形绿地合在一起长为(30﹣3x)m,宽为(24﹣2x)m,根据矩形绿地的面积为480m2 , 即可列出关于x的一元二次方程,解方程即可得出x的值,经检验后得出x=20不符合题意,此题得解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|a|=1,|b|=2,且a>b,则代数式a﹣b的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从地面到高空11千米之间,气温随高度的升高而下降,每升高1千米,气温下降6℃.已知某处地面气温为23℃,设该处离地面 x千米(0<x<11)从的温度为y℃,则y与x的函数关系式为_________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将正方形ABCD(如图1)作如下划分:
第1次划分:分别连接正方形ABCD对边的中点(如图2),得线段HF和EG,它们交于点M,此时图2中共有5个正方形;
第2次划分:将图2左上角正方形AEMH再作划分,得图3,则图3中共有9个正方形;
(1)若每次都把左上角的正方形一次划分下去,则第100次划分后,图中共有______个正方形;
(2)继续划分下去,第几次划分后能有805个正方形?写出计算过程.
(3)能否将正方形性ABCD划分成有2018个正方形的图形?如果能,请算出是第几次划分,如果不能,需说明理由.
(4)如果设原正方形的边长为1,通过不断地分割该面积为1的正方形,并把数量关系和几何图形巧妙地结合起来,可以很容易得到一些计算结果,试着探究求出下面表达式的结果吧.
计算
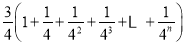 .(直接写出答案即可)
.(直接写出答案即可)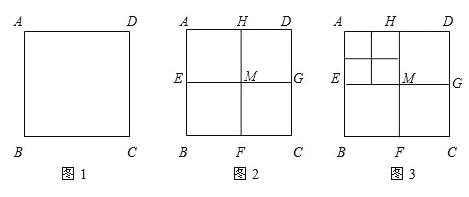
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算﹣a2a3的结果是( )
A.a5B.﹣a5C.﹣a6D.a6
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:6a2b﹣4a3b3﹣2ab
-
科目: 来源: 题型:
查看答案和解析>>【题目】任何实数a,可用[a]表示不超过a的最大整数,如[4]=4,[
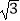 ]=1,现对72进行如下操作:72
]=1,现对72进行如下操作:72  [
[ 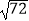 ]=8
]=8  [
[ 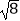 ]=2
]=2 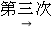 [
[ 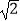 ]=1,这样对72只需进行3次操作即可变为1,类似地,对81只需进行次操作后即可变为1;(2)只需进行3次操作后变为2的所有正整数中,最大的是 .
]=1,这样对72只需进行3次操作即可变为1,类似地,对81只需进行次操作后即可变为1;(2)只需进行3次操作后变为2的所有正整数中,最大的是 .
相关试题

