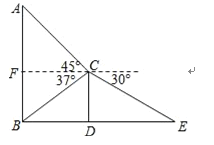
【题目】某班数学兴趣小组为了测量建筑物AB的高度,他们选取了地面上一点E,测得DE的长度为8.65米,并以建筑物CD的顶端点C为观测点,测得点A的仰角为45°,点B的俯角为37°,点E的俯角为30°.

(1)求建筑物CD的高度;
(2)求建筑物AB的高度.
(参考数据:![]() ≈1.73,sin37°≈
≈1.73,sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
参考答案:
【答案】建筑物AB的高度约为11.67米
【解析】
试题分析:(1)由在Rt△CDE中,tan∠CED=![]() ,DE=8.65,∠CED=30°,即可求得答案;
,DE=8.65,∠CED=30°,即可求得答案;
(2)首先过点C作CF⊥AB于点F,然后在Rt△CBF中,求得FC,在Rt△AFC中,求得AF,继而求得答案.
试题解析:(1)在Rt△CDE中,tan∠CED=![]() ,DE=8.65,∠CED=30°,
,DE=8.65,∠CED=30°,
∴tan30°=![]() ,
,
解得:DC≈![]() =5,
=5,
∴建筑物CD的高度约为5米;
(2)过点C作CF⊥AB于点F.
在Rt△CBF中,tan∠FCB=![]() ,BF=DC=5,∠FCB=37°,
,BF=DC=5,∠FCB=37°,
∴tan37°=![]() ≈
≈![]() ,FC≈6.67,
,FC≈6.67,
在Rt△AFC中,∵∠ACF=45°,
∴AF=CF=6.67,
∴AB=AF+BF≈11.67,
∴建筑物AB的高度约为11.67米.
-
科目: 来源: 题型:
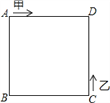
查看答案和解析>>【题目】如图,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若甲的速度是乙的速度的3倍,则它们第2015次相遇在哪条边上( )
A. AB B. BC C. CD D. DA
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OE⊥AB于点O,OF⊥CD于点O,下列结论:
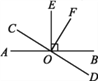
①∠EOF的余角有∠EOC和∠BOF;
②∠EOF=∠AOC=∠BOD;
③∠AOC与∠BOF互为余角;
④∠EOF与∠AOD互为补角.其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果基地积极计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果).如表为装运甲、乙、丙三种水果的重量及利润.
甲
乙
丙
每辆汽车能装的数量(吨)
4
2
3
每吨水果可获利润(千元)
5
7
4
(1)用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用m表示)
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形的两边长是方程x2-6x+8=0的两个根,那么这个等腰三角形的周长是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A是数轴上表示-30的点,B是数轴上表示10的点,C是数轴上表示18的点,点A,B,C在数轴上同时向数轴的正方向运动,点A运动的速度是6个单位长度每秒,点B和C运动的速度是3个单位长度每秒.设三个点运动的时间为t秒(t≠5),设线段OA的中点为P,线段OB的中点为M,线段OC的中点为N,当2PM-PN=2时,t的值为_____.
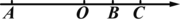
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题提出】已知∠AOB=70°,∠AOD=
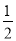 ∠AOC,∠BOD=3∠BOC(∠BOC<45°),求∠BOC的度数.
∠AOC,∠BOD=3∠BOC(∠BOC<45°),求∠BOC的度数.【问题思考】聪明的小明用分类讨论的方法解决.
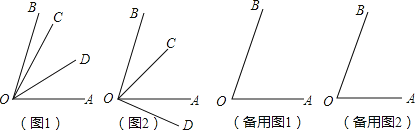
(1)当射线OC在∠AOB的内部时,①若射线OD在∠AOC内部,如图1,可求∠BOC的度数,解答过程如下:
设∠BOC=α,∴∠BOD=3∠BOC=3α,∴∠COD=∠BOD﹣∠BOC=2α,∴∠AOD=
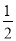 ∠AOC,
∠AOC,∴∠AOD=∠COD=2α,∴∠AOB=∠AOD+∠BOD=2α+3α=5α=70°,∴α=14°,∴∠BOC=14°
问:当射线OC在∠AOB的内部时,②若射线OD在∠AOB外部,如图2,请你求出∠BOC的度数;
【问题延伸】(2)当射线OC在∠AOB的外部时,请你画出图形,并求∠BOC的度数.
【问题解决】综上所述:∠BOC的度数分别是 .
相关试题

