【题目】如图,一次函数y=kx+3的图象分别交x轴、y轴于点B、点C,与反比例函数y= ![]() 的图象在第四象限的相交于点P,并且PA⊥y轴于点A,已知A (0,﹣6),且S△CAP=18.
的图象在第四象限的相交于点P,并且PA⊥y轴于点A,已知A (0,﹣6),且S△CAP=18. 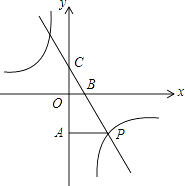
(1)求上述一次函数与反比例函数的表达式;
(2)设Q是一次函数y=kx+3图象上的一点,且满足△OCQ的面积是△BCO面积的2倍,求出点Q的坐标.
参考答案:
【答案】
(1)解:令一次函数y=kx+3中的x=0,则y=3,
即点C的坐标为(0,3),
∴AC=3﹣(﹣6)=9.
∵S△CAP= ![]() ACAP=18,
ACAP=18,
∴AP=4,
∵点A的坐标为(0,﹣6),
∴点P的坐标为(4,﹣6).
∵点P在一次函数y=kx+3的图象上,
∴﹣6=4k+3,解得:k=﹣ ![]() ;
;
∵点P在反比例函数y= ![]() 的图象上,
的图象上,
∴﹣6= ![]() ,解得:n=﹣24.
,解得:n=﹣24.
∴一次函数的表达式为y=﹣ ![]() x+3,反比例函数的表达式为y=﹣
x+3,反比例函数的表达式为y=﹣ ![]()
(2)解:令一次函数y=﹣ ![]() x+3中的y=0,则0=﹣
x+3中的y=0,则0=﹣ ![]() x+3,
x+3,
解得:x= ![]() ,
,
即点B的坐标为( ![]() ,0).
,0).
设点Q的坐标为(m,﹣ ![]()
![]() m+3).
m+3).
∵△OCQ的面积是△BCO面积的2倍,
∴|m|=2× ![]() ,解得:m=±
,解得:m=± ![]() ,
,
∴点Q的坐标为(﹣ ![]() ,9)或(
,9)或( ![]() ,﹣3)
,﹣3)
【解析】(1)由一次函数表达式可得出点C的坐标,结合A点坐标以及三角形的面积公式可得出AP的长度,从而得出点P的坐标,由点P的坐标结合待定系数法即可求出一次函数及反比例函数的表达式;(2)设点Q的坐标为(m,﹣ ![]() m+3).由一次函数的表达式可找出点B的坐标,结合等底三角形面积的性质可得出关于m的一元一次方程,解方程即可得出m的值,将其代入点Q的坐标中即可.
m+3).由一次函数的表达式可找出点B的坐标,结合等底三角形面积的性质可得出关于m的一元一次方程,解方程即可得出m的值,将其代入点Q的坐标中即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),点C在第一象限,对角线BD与x轴平行.直线y=x+4与x轴、y轴分别交于点E,F.将菱形ABCD沿x轴向左平移k个单位,当点C落在△EOF的内部时(不包括三角形的边),k的值可能是( )

A.2 B.3 C.4 D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△BC中,AC=BC,点D、E分别是边AB、AC的中点.延长DE到点F,使DE=EF,得四边形ADCF.若使四边形ADCF是正方形,则应在△ABC中再添加一个条件为_____.
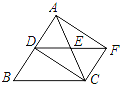
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD,②AD∥BC,③∠B=∠D,④∠D=∠ACB,正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点,第三行有4个点,第四行有8个点,….那么这个三角点阵中前n行的点数之和可能是( )

A. 510 B. 511 C. 512 D. 513
-
科目: 来源: 题型:
查看答案和解析>>【题目】某批发市场有中招考试文具套装,其中A品牌的批发价是每套20元,B品牌的批发价是每套25元,小王需购买A、B两种品牌的文具套装共1000套.
(1)若小王按需购买A、B两种品牌文具套装共用22000元,则各购买多少套?
(2)凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元.若小王购买会员卡并用此卡按需购买1000套文具套装,共用了y元,设A品牌文具套装买了x包,请求出y与x之间的函数关系式.
(3)若小王购买会员卡并用此卡按需购买1000套文具套装,共用了20000元,他计划在网店包邮销售这两种文具套装,每套文具套装小王需支付邮费8元,若A品牌每套销售价格比B品牌少5元,请你帮他计算,A品牌的文具套装每套定价不低于多少元时才不亏本(运算结果取整数)? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AC=10m,BC=6m,且它们在同一条直线上,点M、N分别为线段AC和BC的中点,则线段MN的长为_____
相关试题

