【题目】汽车公司有甲、乙两种货车可供租用,现有一批货物要运往某地,货主准备租用该公司货车,已知以往甲、乙两种货车运货情况如下表:
第一次 | 第二次 | |
甲种货车(辆) | 2 | 5 |
乙种货车(辆) | 3 | 6 |
累计运货(吨) | 13 | 28 |
(1)甲、乙两种货车每辆可装多少吨货物?
(2)若货主需要租用该公司的甲种货车8辆,乙种货车6辆,刚好运完这批货物,如按每吨付运费50元,则货主应付运费总额为多少元?
(3)若货主共有20吨货,计划租用该公司的货车正好(每辆车都满载)把这批货运完,该汽车公司共有哪几种运货方案?
参考答案:
【答案】(1)甲、乙两种货车每辆可分别装2吨、3吨;(2)货主应付货款1700元;(3)共有如下表所示的四种方案:
方案一 | 方案二 | 方案三 | 方案四 | |
甲种货车(辆) | 10 | 7 | 4 | 1 |
乙种货车(辆) | 0 | 2 | 4 | 6 |
【解析】1、分析题意,易知本题需了方程组求解,解答本题需知道1辆甲种货车,1辆乙种货车一次运货吨数,想想如何求解;
2、可得等量关系为:2辆甲种货车运货吨数+3辆乙种货车运货吨数=13,5辆甲种货车运货吨数+6辆乙种货车运货吨数=28;根据等量关系列方程自己可求得1辆甲种货车,1辆乙种货车一次运货吨数;
3、接下来根据“现租用该公司8辆甲种货车及6辆乙种货车一次刚好运完这批货,如果按每吨付运费50元计算”列式计算即可.
本题解析:(1)设甲种货车每辆可装x吨,乙种货车每辆可装y吨.
根据题意,得![]() 解方程组得
解方程组得![]()
答:甲、乙两种货车每辆可分别装2吨、3吨;
(2)50×(8×2+6×3)=1700(元).
答:货主应付货款1700元;
(3)设租用甲种货车共a辆,乙种货车b辆.
根据题意,得2a+3b=20,此方程的非负整数解共有四个: ![]()
![]()
![]()
![]() 答:共有如下表所示的四种方案:
答:共有如下表所示的四种方案:
方案一 | 方案二 | 方案三 | 方案四 | |
甲种货车(辆) | 10 | 7 | 4 | 1 |
乙种货车(辆) | 0 | 2 | 4 | 6 |
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店以每套80元的进价购进8套服装,并以90元左右的价格卖出.如果以90元为标准,超过标准的售价记为正数,不足标准的售价记为负数,出售价格记录如下:+2,﹣3,+5,+1,﹣2,﹣1,0,﹣5(单位:元).其它收支不计,当商店卖完这8套服装后( )
A. 盈利 B. 亏损 C. 不盈不亏 D. 盈亏不明
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面几何体的截面图可能是圆的是( )
A. 圆锥 B. 正方体 C. 长方体 D. 棱柱
-
科目: 来源: 题型:
查看答案和解析>>【题目】幼儿园的小朋友打算选择一种形状、大小都相同的多边形塑料胶板铺地面.为了保证铺地时既无缝隙,又不重叠,请你告诉他们可以选择哪些形状的塑料胶板(填三种) .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为1的小正方形网格中,△AOB的顶点均在格点上.

(1)B点关于y轴的对称点坐标为 ;
(2)将△AOB向左平移3个单位长度,再向上平移2个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)的条件下,△AOB边AB上有一点P的坐标为(a,b),则平移后对应点P1的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校规划在一块长AD为18m,宽AB为13m的长方形场地ABCD上,设计分别与AD,AB平行的横向通道和纵向通道,其余部分铺上草皮.
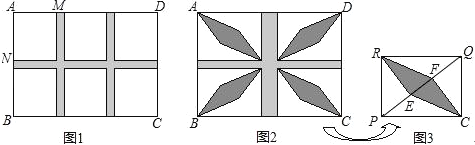
(1)如图1,若设计三条通道,一条横向,两条纵向,且它们的宽度相等,其余六块草坪相同,其中一块草坪两边之比AM:AN=8:9,问通道的宽是多少?
(2)为了建造花坛,要修改(1)中的方案,如图2,将三条通道改为两条通道,纵向的宽度改为横向宽度的2倍,其余四块草坪相同,且每一块草坪均有一边长为8m,这样能在这些草坪建造花坛.如图3,在草坪RPCQ中,已知RE⊥PQ于点E,CF⊥PQ于点F,求花坛RECF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.
(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)

相关试题

