Question

【题目】抛物线y＝ax2＋c与x轴交于A、B两点，顶点为C，点P为抛物线上，且位于x轴下方．

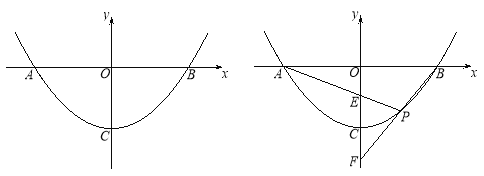
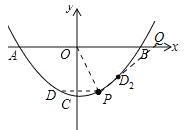
（1）如图1，若P（1，－3）、B（4，0），

① 求该抛物线的解析式；

② 若D是抛物线上一点，满足∠DPO＝∠POB，求点D的坐标；

（2） 如图2，已知直线PA、PB与y轴分别交于E、F两点．当点P运动时，是否为定值？若是，试求出该定值；若不是，请说明理由．

Answer 1

【答案】（1）①y＝x2-；②点D的坐标为（-1，-3）或（，）；（2）是定值，等于2.

【解析】

试题分析：（1）①将P（1，－3）、B（4，0）代入y＝ax2＋c得方程组，解方程组即可求得a、c的值，就求得函数解析式；②分两种情况求得点D的坐标即可；（2）设B（b，0），则A（-b，0）有ab2＋c＝0，即可得b2＝，过点P（x0，y0）作PH⊥AB，有，利用相似三角形的性质分别求得OE、OF的值，即可得的值.

试题解析：（1）①将P（1，－3）、B（4，0）代入y＝ax2＋c得

，解得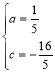 ，抛物线的解析式为： ．

②如图：

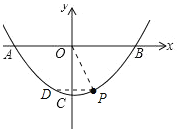
由∠DPO＝∠POB得DP∥OB，D与P关于y轴对称，P（1，－3）得D（-1，-3）；

如图，D在P右侧，即图中D2，则∠D2PO＝∠POB，延长PD2交x轴于Q，则QO＝QP，

设Q（q，0），则（q－1）2＋32＝q2，解得：q＝5，∴Q（5，0），则直线PD2为 ，再联立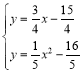 得：x＝1或 ，∴ D2（ ）

∴点D的坐标为（-1，-3）或（ ）

（2）设B（b，0），则A（-b，0）有ab2＋c＝0，∴b2＝，过点P（x0，y0）作PH⊥AB，有，易证：△PAH∽△EAO，则 即，∴，

同理得∴，∴，则OE＋OF＝

∴，又OC＝－c,∴.

∴是定值，等于2．