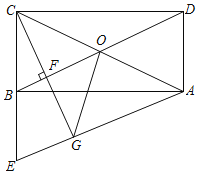
【题目】如图,在矩形ABCD中,AC、BD相交于点O,过点A作BD的平行线AE交CB的延长线于点E.
(1)求证:BE=BC;
(2)过点C作CF⊥BD于点F,并延长CF交AE于点G,连接OG.若BF=3,CF=6,求四边形BOGE的周长.
参考答案:
【答案】(1)详见解析;(2)3![]() +21.
+21.
【解析】
(1)利用平行线等分线段定理证明即可.
(2)根据勾股定理得BC=![]() ,易证△CBF∽△DBC,得BD=15,根据矩形的性质和直角三角形的性质得OG=
,易证△CBF∽△DBC,得BD=15,根据矩形的性质和直角三角形的性质得OG=![]() ,利用平行线等分线段定理得BE=3
,利用平行线等分线段定理得BE=3![]() ,由中位线的性质得EG=6,进而即可求解.
,由中位线的性质得EG=6,进而即可求解.
(1)∵四边形ABCD是矩形,
∴OC=OA,
∵OB∥AE,
∴BC=BE;
(2)∵CF⊥BD,
∴∠CFB=90°,
在Rt△BCF中,BC=![]() ,
,
∵四边形ABCD是矩形,
∴∠BCD=90°=∠BFC,AC=BD,
∵∠CBF=∠DBC,
∴△CBF∽△DBC,
∴![]() ,
,
∴BD=![]() =15,OB=OD=
=15,OB=OD=![]() ,
,
∴AC=BD=15,
∵CF⊥BD,BD∥AE,
∴CG⊥AE,
∴∠AGC=90°,
∵OC=OA,
∴OG=![]() AC=
AC=![]() ,
,
∵OC=OA,OF∥AG,
∴CF=FG,
∴BC=BE=3![]() ,
,
∴EG=2BF=6,
∴四边形BOGE的周长=3![]() +6+
+6+![]() +
+![]() =3
=3![]() +21.
+21.
-
科目: 来源: 题型:
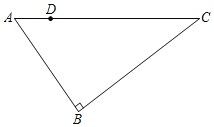
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,点D为AC边上的个动点,点D从点A出发,沿边AC向C运动,当运动到点C时停止,设点D运动时间为t秒,点D运动的速度为每秒1个单位长度的.
(1)当t=2时,求CD的长;
(2)求当t为何值时,线段BD最短?
-
科目: 来源: 题型:
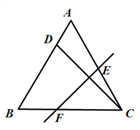
查看答案和解析>>【题目】已知D是等边△ABC边AB上的一点,现将△ABC折叠,使点C与D重合,折痕为EF,点E、
F分别在AC和BC上.如图,若AD∶DB=1∶4,则CE∶CF=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某经销商从市场得知如下信息:
某品牌空调扇
某品牌电风扇
进价(元/台)
700
100
售价(元/台)
900
160
他现有40000元资金可用来一次性购进该品牌空调扇和电风扇共100台,设该经销商购进空调扇
 台,空调扇和电风扇全部销售完后获得利润为
台,空调扇和电风扇全部销售完后获得利润为 元.
元.(1)求
 关于
关于 的函数解析式;
的函数解析式;(2)利用函数性质,说明该经销商如何进货可获利最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 中,AB=AC,AB 的垂直平分线交 AB 于点 D,交 CA 的延长线于点 E,∠EBC=42°,则 ∠BAC=( )

A. 159° B. 154° C. 152° D. 138°
-
科目: 来源: 题型:
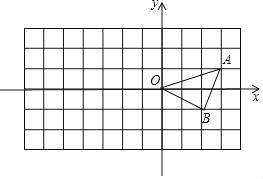
查看答案和解析>>【题目】方格纸中每个小正方形的边长都是单位1,△OAB在平面直角坐标系中的位置如图所示.解答问题:
(1)请按要求对△ABO作如下变换:
①将△OAB向下平移2个单位,再向左平移3个单位得到△O1A1B1;
②以点O为位似中心,位似比为2:1,将△ABC在位似中心的异侧进行放大得到△OA2B2.
(2)写出点A1,A2的坐标: , ;
(3)△OA2B2的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点C,交AB的延长线于点E,连接CD、CE.
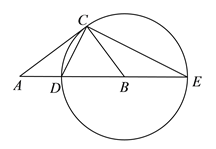
(1)求证:△ACD∽△AEC;
(2)当
 时,求tanE;
时,求tanE;(3)若AD=4,AC=4
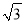 ,求△ACE的面积.
,求△ACE的面积.
相关试题

