Question

【题目】在四边形ABCD中,AC交BD于点O,且AB∥CD,给出以下四种说法:
①如果再加上条件“BC=AD”,那么四边形ABCD一定是平行四边形;
②如果再加上条件“∠BAD=∠BCD”,那么四边形ABCD一定是平行四边形;
③如果再加上条件“AO=OC”,那么四边形ABCD一定是平行四边形;
④如果再加上条件“∠DBA=∠CAB”,那么四边形ABCD一定是平行四边形.
其中正确的说法是( )
A.①②
B.①③④
C.②③
D.②③④

Answer 1

【答案】C
【解析】如图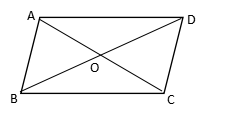

①当AB∥CD，BC=AD，不能判定四边形ABCD是平行四边形；因此①不符合题意；
②∵AB∥CD
∴∠ABD=∠CDB
在△ABD和△CBD中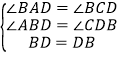

∴△ABD≌△CBD
∴AB=CD AB∥CD
∴四边形ABCD是平行四边形，因此②符合题意；
③∵AB∥CD
∴∠ABD=∠CDB
在△ABO和△CDO中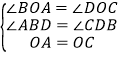

∴△ABO≌△CDO
∴AB=CD AB∥CD
∴四边形ABCD是平行四边形，因此③符合题意；
④如果再加上条件“∠DBA=∠CAB”,不能判定四边形ABCD是平行四边形，因此④不符合题意；
所以正确的说法有②③
故答案为：C
平行四边形的五种判定方法分别是：（1）两组对边分别平行的四边形是平行四边形；（2）两组对边分别相等的四边形是平行四边形；（3）一组对边平行且相等的四边形是平行四边形；（4）两组对角分别相等的四边形是平行四边形；（5）对角线互相平分的四边形是平行四边形．根据平行四边形的判定，加上四选项中的条件，逐一进行验证。