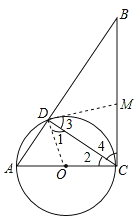
【题目】在RT△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,连接CD.

(1)求证:∠DCB=∠A;
(2)若M为线段BC上一点,试问点M在什么位置时,直线DM与⊙O相切?并说明理由。
参考答案:
【答案】(1)证明见解析;(2)当MC=MD(或点M是BC的中点)时,直线DM与⊙O相切.理由见解析.
【解析】
试题分析:(1)根据圆周角定理可得∠ADC=90°,再根据直角三角形的性质可得∠A+∠DCA=90°,再由∠DCB+∠ACD=90°,可得∠DCB=∠A;
(2)当MC=MD时,直线DM与⊙O相切,连接DO,根据等等边对等角可得∠1=∠2,∠4=∠3,再根据∠ACB=90°可得∠1+∠3=90°,进而证得直线DM与⊙O相切.
试题解析:(1)∵AC为直径,
∴∠ADC=90°,
∴∠A+∠DCA=90°,
∵∠ACB=90°,
∴∠DCB+∠ACD=90°,
∴∠DCB=∠A;
(2)当MC=MD(或点M是BC的中点)时,直线DM与⊙O相切;
连接DO,
∵DO=CO,
∴∠1=∠2,
∵DM=CM,
∴∠4=∠3,
∵∠2+∠4=90°,
∴∠1+∠3=90°,
∴直线DM与⊙O相切,
故当MC=MD(或点M是BC的中点)时,直线DM与⊙O相切.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的周长是40 cm,腰长y(cm)是底边长x(cm)的函数.此函数的表达式和自变量取值范围正确的是( )
A. y=-2x+40(0<x<20)B. y=-0.5x+20(10<x<20)
C. y=-2x+40(10<x<20)D. y=-0.5x+20(0<x<20)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果盈利15元记作+15,那么亏本51元记作( )
A.+51元
B.﹣51元
C.+15元
D.﹣15 -
科目: 来源: 题型:
查看答案和解析>>【题目】
①1是绝对值最小的数;
②0既不是正数,也不是负数;
③一个有理数不是整数就是分数;
④0的绝对值是0.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形。若
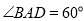 ,AB=2,则图中阴影部分的面积为______.
,AB=2,则图中阴影部分的面积为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为___________

-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形
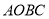 中,
中,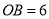 ,
,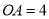 .分别以
.分别以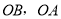 所在直线为
所在直线为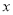 轴和
轴和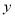 轴,建立如图所示的平面直角坐标系.
轴,建立如图所示的平面直角坐标系.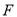 是边
是边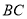 上一点,过点
上一点,过点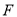 的反比例函数
的反比例函数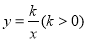 图象与
图象与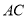 边交于点
边交于点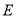 .
.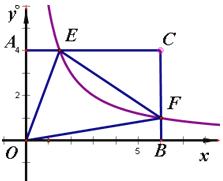
(1)请用k表示点E,F的坐标;
(2)若
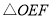 的面积为
的面积为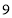 ,求反比例函数的解析式.
,求反比例函数的解析式.
相关试题

