【题目】如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径.

参考答案:
【答案】小桥所在圆的半径为5m.
【解析】
试题分析:根据已知得出旗杆高度,进而得出GM=MH,再利用勾股定理求出半径即可.
解:∵小刚身高1.6米,测得其影长为2.4米,
∴8米高旗杆DE的影子为:12m,
∵测得EG的长为3米,HF的长为1米,
∴GH=12﹣3﹣1=8(m),
∴GM=MH=4m.
如图,设小桥的圆心为O,连接OM、OG.
设小桥所在圆的半径为r,
∵MN=2m,
∴OM=(r﹣2)m.
在Rt△OGM中,由勾股定理得:
∴OG2=OM2+42,
∴r2=(r﹣2)2+16,
解得:r=5,
答:小桥所在圆的半径为5m.

-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形、菱形、正方形都是特殊的四边形,它们具有很多共性,如:_________.(填一条既可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知DC∥FP,∠1=∠2,∠FED=28,∠AGF=80,FH平分∠EFG.
(1)说明:DC∥AB;
(2)求∠PFH的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为响应国家的“节能减排”政策,某厂家开发了一种新型的电动车,如图,它的大灯A射出的光线AB、AC与地面MN的夹角分别为22°和31°,AT⊥MN,垂足为T,大灯照亮地面的宽度BC的长为
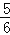 m.
m.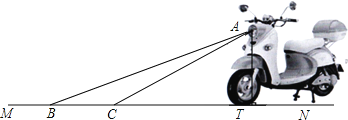
(1)求BT的长(不考虑其他因素).
(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2s,从发现危险到电动车完全停下所行驶的距离叫做最小安全距离.某人以20km/h的速度驾驶该车,从做出刹车动作到电动车停止的刹车距离是
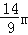 ,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.
,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.(参考数据:sin22°≈
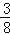 ,tan22°≈
,tan22°≈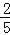 ,sin31°≈
,sin31°≈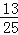 ,tan31°≈
,tan31°≈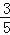 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】把二次函数y=(x﹣1)2+2的图象绕原点旋转180°后得到的图象的解析式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A在x轴的上方,在y轴的左侧,且距离x轴3个单位,且距离y轴4个单位,那么A点的坐标是( )
A. (-4,3) B. (4,-3) C. (-3,4) D. ( -4, -3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一种袋装大米上标有10±0.3kg,则下列四袋大米中,不符合标准的是( )
袋号
一
二
三
四
质量/kg
10.2
9.7
9.9
9.6
A、第一袋 B、第二袋 C、第三袋 D、第四袋
相关试题

