【题目】如图,已知正方形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,抛物线y=![]() x2+bx+c经过点A,B,交正x轴于点D,E是OC上的动点(不与C重合)连接EB,过B点作BF⊥BE交y轴与F
x2+bx+c经过点A,B,交正x轴于点D,E是OC上的动点(不与C重合)连接EB,过B点作BF⊥BE交y轴与F
(1)求b,c的值及D点的坐标;
(2)求点E在OC上运动时,四边形OEBF的面积有怎样的规律性?并证明你的结论;
(3)连接EF,BD,设OE=m,△BEF与△BED的面积之差为S,问:当m为何值时S最小,并求出这个最小值.

参考答案:
【答案】(1)b=![]() ,c=2;D点坐标为(3,0).(2)点E在OC上运动时,四边形OEBF的面积不变;(3)当m=2﹣
,c=2;D点坐标为(3,0).(2)点E在OC上运动时,四边形OEBF的面积不变;(3)当m=2﹣![]() 时S最小为0.
时S最小为0.
【解析】
试题分析:(1)把点A,B代入抛物线y=![]() x2+bx+c求得b、c即可,y=0,建立方程求得点D;
x2+bx+c求得b、c即可,y=0,建立方程求得点D;
(2)四边形OEBF的面积不变,利用三角形全等证得结论即可;
(3)用m分别表示出两个三角形的面积,求差探讨得出答案即可.
试题解析:(1)把点A(0,2)、B(2,2)代入抛物线y=![]() x2+bx+c得
x2+bx+c得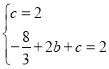
解得b=![]() ,c=2;
,c=2;
∴y=![]() x2+
x2+![]() x+2;
x+2;
令![]() x2+
x2+![]() x+2=0
x+2=0
解得x1=﹣1,x2=3
∴D点坐标为(3,0).
(2)点E在OC上运动时,四边形OEBF的面积不变;
∵四边形OABC是正方形
∴AB=BC,∠BCE=∠BAE=∠ABC=90°
又∵BF⊥BE
∴∠FBE=90°
∴∠ABF=∠CBE
∴△ABF≌△BCE
∴四边形OEBF的面积始终等于正方形OABC的面积.
(3)如图,
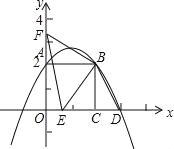
可以看出S△BEF=S梯形OCBF﹣S△OEF﹣S△BEC
=![]() (2+2+m)×2﹣
(2+2+m)×2﹣![]() m(2+m)﹣
m(2+m)﹣![]() (2﹣m)×2
(2﹣m)×2
=﹣![]() m2+m+2
m2+m+2
S△BED=![]() ×(3﹣m)×2
×(3﹣m)×2
=3﹣m
两个三角形的面积差最小为0,
即3﹣m=﹣![]() m2+m+,
m2+m+,
解得m=2±![]() ,
,
∵E是OC上的动点
∴m=2﹣![]() ,
,
当m=2﹣![]() 时S最小为0.
时S最小为0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(﹣1,0).有下列结论:
①abc>0;②4a﹣2b+c<0;③4a+b=0;④抛物线与x轴的另一个交点是(5,0);⑤点(﹣3,y1),(6,y2)都在抛物线上,则有y1<y2.
其中正确的是( )
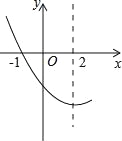
A.①②③ B.②④⑤ C.①③④ D.③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=3是关于x的方程2x﹣k=4的解,则k的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个大型模板,设计要求BA与CD相交成30°角,DA与CB相交成20°角,怎样通过测量∠A,∠B,∠C,∠D的度数,来检验模板是否合格?
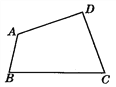
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2-mx+36是一个完全平方式,则m=____________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程x2﹣2x+m=0有一个解为x=﹣1,则m的值为( )
A. 1B. ﹣3C. 3D. 4
-
科目: 来源: 题型:
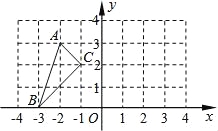
查看答案和解析>>【题目】如图,△ABC的顶点都在方格线的交点(格点)上.
(1)将△ABC绕C点按逆时针方向旋转90°得到△A′B′C′,请在图中画出△A′B′C′.
(2)将△ABC向上平移1个单位,再向右平移5个单位得到△A″B″C″,请在图中画出△A″B″C″.
(3)若将△ABC绕原点O旋转180°,A的对应点A1的坐标是 .
相关试题

