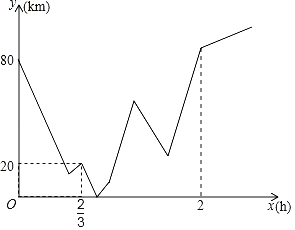
【题目】A、B两地之间有一修理厂C,一日小海和王陆分别从A、B两地同时出发相向而行,王陆开车,小海骑摩托.二人相遇时小海的摩托车突然出故障无法前行,王陆决定将小海和摩托车一起送回到修理厂C后再继续按原路前行,王陆到达A地后立即返回B地,到B地后不再继续前行,等待小海前来(装载摩托车时间和掉头时间忽略不计),整个行驶过程中王陆速度不变,而小海在修理厂花了十分钟修好摩托车,为了赶时间,提速![]() 前往目的地B,小海到达B地后也结束行程,若图象表示的是小海与王陆二人到修理厂C的距离和y(km)与小海出行时间之间x(h)的关系,则当王陆第二次与小海在行驶中相遇时,小海离目的地B还有_____km.
前往目的地B,小海到达B地后也结束行程,若图象表示的是小海与王陆二人到修理厂C的距离和y(km)与小海出行时间之间x(h)的关系,则当王陆第二次与小海在行驶中相遇时,小海离目的地B还有_____km.
参考答案:
【答案】14
【解析】
从![]() 时,
时,![]() 得
得![]() 、
、![]() 两地距离为
两地距离为![]() ,再从
,再从![]() ,
,![]() 得,第一次相遇点与
得,第一次相遇点与![]() 点距离为
点距离为![]() ,根据题意与函数图象知,当
,根据题意与函数图象知,当![]() 时,王陆回到了
时,王陆回到了![]() 点,进而求得王陆的速度,再根据相遇问题求出两人的速度和,进而得小海的速度,设把摩托车送回到修理厂
点,进而求得王陆的速度,再根据相遇问题求出两人的速度和,进而得小海的速度,设把摩托车送回到修理厂![]() 后,再过
后,再过![]() ,两人第二次相遇,根据追及问题列出方程求得
,两人第二次相遇,根据追及问题列出方程求得![]() ,进而求得第二次相遇时,他们距
,进而求得第二次相遇时,他们距![]() 地的距离,即可求得结果.
地的距离,即可求得结果.
解:从函数图象可知,∵x=0h时,y=80km,
∴AB=80km,
设两人第一次相遇地点为D地,
∵x=![]() h,y=20km,
h,y=20km,
∴BD﹣BC=20÷2=10(km),
由函数图象可知,当时间x=2h时,王陆回到了B地,
∴王陆的速度为:(80×2+10×2)÷2=90(km/h),
∴小海原来的速度为:80÷![]() ﹣90=30(km/h),
﹣90=30(km/h),
小海后来的速度为:30×(1+![]() )=40(km/h),
)=40(km/h),
设把摩托车送回到修理厂C后,再过ah,两人第二次相遇,则
90a=[30×![]() +10]×2+40(a﹣﹣
+10]×2+40(a﹣﹣![]() ),
),
∴a=![]() ,
,
∴当王陆第二次与小海在行驶中相遇时,小海离目的地B的距离为:
80﹣[30×![]() +10+40(a﹣﹣
+10+40(a﹣﹣![]() )]=14.
)]=14.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的分式方程
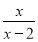 ﹣
﹣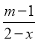 =3的解为正整数,且关于y的不等式组
=3的解为正整数,且关于y的不等式组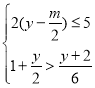 至多有六个整数解,则符合条件的所有整数m的取值之和为( )
至多有六个整数解,则符合条件的所有整数m的取值之和为( )A.1B.0C.5D.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠ACB=45°,D为AC上一点,AD=5
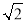 ,连接BD,将△ABD沿BD翻折至△EBD,点A的对应点E点恰好落在边BC上.延长BC至点F,连接DF,若CF=2,tan∠ABD=
,连接BD,将△ABD沿BD翻折至△EBD,点A的对应点E点恰好落在边BC上.延长BC至点F,连接DF,若CF=2,tan∠ABD=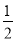 ,则DF长为( )
,则DF长为( )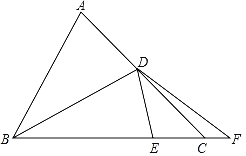
A.
 B.
B.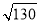 C.5
C.5 D.7
D.7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD的对角线AC与BD相交于点O,按以下步骤作图:①以点A为圆心,以任意长为半径作弧,分别交AO,AB于点M,N;②以点O为圆心,以AM长为半径作弧,交OC于点M';③以点M'为圆心,以MN长为半径作弧,在∠COB内部交前面的弧于点N';④过点N'作射线ON'交BC于点E.若AB=8,则线段OE的长为_______.
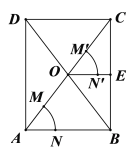
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
a.七年级成绩频数分布直方图:

b.七年级成绩在
 这一组的是:70 72 74 75 76 76 77 77 77 78 79
这一组的是:70 72 74 75 76 76 77 77 77 78 79c.七、八年级成绩的平均数、中位数如下:
年级
平均数
中位数
七
76.9
m
八
79.2
79.5
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在80分以上(含80分)的有 人;
(2)表中m的值为 ;
(3)在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;
(4)该校七年级学生有400人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
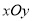 中,一次函数
中,一次函数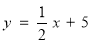 和
和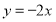 的图象相交于点
的图象相交于点 ,反比例函数
,反比例函数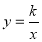 的图象经过点
的图象经过点 .
.(1)求反比例函数的表达式;
(2)设一次函数
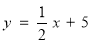 的图象与反比例函数
的图象与反比例函数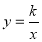 的图象的另一个交点为
的图象的另一个交点为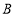 ,连接
,连接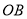 ,求
,求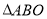 的面积.
的面积.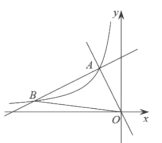
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人加工同一种零件,甲每天加工的数量是乙每天加工数量的 1.5 倍,两人各加工 600 个这种零件,甲比乙少用 5 天.
(1)求甲、乙两人每天各加工多少个这种零件?
(2)已知甲、乙两人加工这种零件每天的加工费分别是 150 元和 120 元,现有 3000 个这种零件的加工任务,甲单独加工一段时间后另有安排,剩余任务由乙单独完成.如果总加工费不超过 7800 元,那么甲至少加工了多少天?
相关试题

