【题目】如图,点A是双曲线y= ![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 . 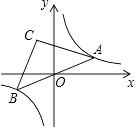
参考答案:
【答案】y=﹣ ![]()
【解析】解:如图,连结OC,作CD⊥x轴于D,AE⊥x轴于E,
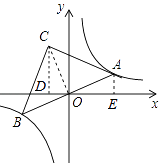
∵A点、B点是正比例函数图象与双曲线y= ![]() 的交点,
的交点,
∴点A与点B关于原点对称,
∴OA=OB,
∵△ABC为等腰直角三角形,
∴OC=OA,OC⊥OA,
∴∠DOC+∠AOE=90°,
∵∠DOC+∠DCO=90°,
∴∠DCO=∠AOE,
∵在△COD和△OAE中,
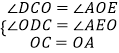 ,
,
∴△COD≌△OAE(AAS),
设A点坐标为(a, ![]() ),则OD=AE=
),则OD=AE= ![]() ,CD=OE=a,
,CD=OE=a,
∴C点坐标为(﹣ ![]() ,a),
,a),
∵﹣ ![]() a=﹣8,
a=﹣8,
∴点C在反比例函数y=﹣ ![]() 图象上.
图象上.
故答案为:y=﹣ ![]() .
.
连结OC,作CD⊥x轴于D,AE⊥x轴于E,先证明△COD≌△OAE,设出点A的坐标(a, ![]() ),表示出OD、CD的长,从而得到点C的坐标,从而求得C点所在的函数图像的解析式.
),表示出OD、CD的长,从而得到点C的坐标,从而求得C点所在的函数图像的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】满足下列条件的△ABC,不是直角三角形的是( )
A. b2=a2﹣c2 B. a:b:c=3:4:5
C. ∠C=∠A﹣∠B D. ∠A:∠B:∠C=3:4:5
-
科目: 来源: 题型:
查看答案和解析>>【题目】【新知理解】
如图①,点C在线段AB上,图中共有三条线段AB、AC和BC,若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“巧点”.
线段的中点__________这条线段的“巧点”;(填“是”或“不是”).
若AB = 12cm,点C是线段AB的巧点,则AC=___________cm;
【解决问题】
(3) 如图②,已知AB=12cm.动点P从点A出发,以2cm/s的速度沿AB向点B匀速移动:点Q从点B出发,以1cm/s的速度沿BA向点A匀速移动,点P、Q同时出发,当其中一点到达终点时,运动停止,设移动的时间为t(s).当t为何值时,A、P、Q三点中其中一点恰好是另外两点为端点的线段的巧点?说明理由


-
科目: 来源: 题型:
查看答案和解析>>【题目】本学期学校开展以“感受中华传统美德”为主题的研学活动,组织150名学生参观历史博物馆和民俗展览馆,每一名学生只能参加其中一项活动,共支付票款2000元,票价信息如下:
地点
票价
历史博物馆
10元/人
民俗展览馆
20元/人
(1)请问参观历史博物馆和民俗展览馆的人数各是多少人?
(2)若学生都去参观历史博物馆,则能节省票款多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年12月份,我市迎来国家级文明城市复查,为了了解学生对文明城市的了解情况,学校随机抽取了部分学生进行问卷调查,将调查结果技照“A非常了解
 了解
了解 了解较少
了解较少 不了解”四类分别统计,并绘制了下列两幅统计图
不了解”四类分别统计,并绘制了下列两幅统计图 不完整
不完整 请根据图中信息,解答下列问题:
请根据图中信息,解答下列问题: 此次共调查了______名学生;
此次共调查了______名学生; 扇形统计图中D所在的扇形的圆心角为______;
扇形统计图中D所在的扇形的圆心角为______; 将条形统计图补充完整;
将条形统计图补充完整; 若该校共有800名学生,请你估计对文明城市的了解情况为“非常了解”的学生的人数.
若该校共有800名学生,请你估计对文明城市的了解情况为“非常了解”的学生的人数.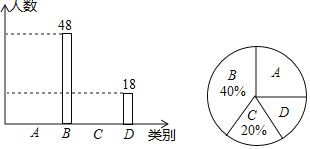
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲所示,若将阴影两部分裁剪下来重新拼成一个正方形,所拼正方形如图乙.

 图甲的长是______,宽是______,面积是______
图甲的长是______,宽是______,面积是______ 写成两式乘积形式
写成两式乘积形式 ;如图乙所示,阴影部分的面积是______
;如图乙所示,阴影部分的面积是______ 写成多项式的形式
写成多项式的形式
 比较图甲和图乙中阴影部分的面积,可得乘法公式______.
比较图甲和图乙中阴影部分的面积,可得乘法公式______. 运用你所得到的公式,计算下列各题:
运用你所得到的公式,计算下列各题: ;
; ;
;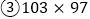 .
. -
科目: 来源: 题型:
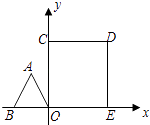
查看答案和解析>>【题目】如图,边长为1的正△ABO的顶点O在原点,点B在x轴负半轴上,正方形OEDC边长为2,点C在y轴正半轴上,动点P从点A出发,以每秒1个单位的速度沿着△ABO的边按逆时针方向运动,动点Q从D点出发,以每秒1个单位的速度沿着正方形OEDC的边也按逆时针方向运动,点Q比点P迟1秒出发,则点P运动2016秒后,则PQ2的值是 .
相关试题

