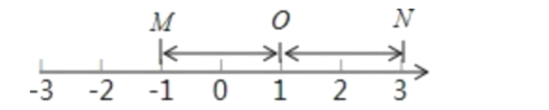
【题目】在数轴上,把表示数1的点称为基准点,记作点![]() .对于两个不同的点M和N,若点M、点N到点
.对于两个不同的点M和N,若点M、点N到点![]() 的距离相等,则称点M与点N互为基准变换点.例如:图1中,点M表示数-1,点N表示数3,它们与基准点
的距离相等,则称点M与点N互为基准变换点.例如:图1中,点M表示数-1,点N表示数3,它们与基准点![]() 的距离都是2个单位长度,点M与点N互为基准变换点.
的距离都是2个单位长度,点M与点N互为基准变换点.
(1)已知点A表示数a,点B表示数b,点A与点B互为基准变换点.
①若a=0,则b=_________;若a=4,则b=_________;
②用含a的式子表示b,则b=____________;
(2)对点A进行如下操作:先把点A表示的数乘以2.5,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B. 若点A与点B互为基准变换点,则点A表示的数是___________;
(3)点P在点Q的左边,点P与点Q之间的距离为8个单位长度.对P、Q两点做如下操作:点P沿数轴向右移动k(k>0)个单位长度得到![]() ,
,![]() 为
为![]() 的基准变换点,点
的基准变换点,点![]() 沿数轴向右移动k个单位长度得到
沿数轴向右移动k个单位长度得到![]() ,
,![]() 为
为![]() 的基准变换点,…,依此顺序不断地重复,得到
的基准变换点,…,依此顺序不断地重复,得到![]() ,
,![]() ,…,
,…,![]() .
.![]() 为Q的基准变换点,将数轴沿原点对折后
为Q的基准变换点,将数轴沿原点对折后![]() 的落点为
的落点为![]() ,
,![]() 为
为![]() 的基准变换点,将数轴沿原点对折后
的基准变换点,将数轴沿原点对折后![]() 的落点为
的落点为![]() ,…,依此顺序不断地重复,得到
,…,依此顺序不断地重复,得到![]() ,
,![]() ,…,
,…,![]() .若无论k为何值,
.若无论k为何值,![]() 与
与![]() 两点间的距离都是4,则n=__________
两点间的距离都是4,则n=__________
参考答案:
【答案】2 ![]()
![]()
![]() 4或12
4或12
【解析】
(1)①根据互为基准变换点的定义可得出a+b=2,代入数据即可得出结论;
②根据a+b=2,变换后即可得出结论;
(2)设点A表示的数为x,根据点A的运动找出点B,结合互为基准变换点的定义即可得出关于x的一元一次方程,解之即可得出结论;
(3)根据点Pn与点Qn的变化找出变化规律“P4n-1=2-m,Q4n-1=-m+4n-8;P4n=m、Q4n=m+8-4n”,再根据两点间的距离公式即可得出关于n的含绝对值符号的一元一次方程,解之即可得出结论.
解:(1)①∵点A表示数a,点B表示数b,点A与点B互为基准变换点,
∵a+b=2.
当a=0时,b=2;
当a=4时,b=-2.
故答案为:2;-2.
②∵a+b=2,
∴b=2-a.
故答案为:2-a.
(2)设点A表示的数为x,
根据题意得:![]() ,
,
解得:![]() .
.
故答案为:![]() .
.
(3)设点P表示的数为m,则点Q表示的数为m+8,
由题意可知:P1表示的数为m+k,P2表示的数为2-(m+k),P3表示的数为2-m,P4表示的数为m,P5表示的数为m+k,…,
Q1表示的数为:-m-6,Q2表示的数为:m+6,Q3表示的数为:-m-4,Q4表示的数为:m+4,Q5表示的数为:-m-2,Q6表示的数为:m+2,…,
∴P4n-1=2-m,Q4n-1=-m+4n-8;P4n=m,Q4n=m+8-4n.
①|2-m-(-m+4n-8)|=4,即|-4n+10|=4,
解得:4n=6或4n=14,
又∵n为正整数,
∴4n为4的倍数,
∴6和14不符合题意,舍去;
②令|m-(m+8-4n)|=4,即|8-4n|=4,
解得:4n=4或4n=12.
故答案为:4或12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
(1)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的
 ,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(7分)某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).
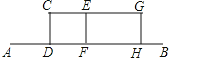
(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法);
(2)求小明原来的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某次海上军事学习期间,我军为确保△OBC海域内的安全,特派遣三艘军舰分别在O、B、C处监控△OBC海域,在雷达显示图上,军舰B在军舰O的正东方向80海里处,军舰C在军舰B的正北方向60海里处,三艘军舰上装载有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域.(只考虑在海平面上的探测)
(1)若三艘军舰要对△OBC海域进行无盲点监控,则雷达的有效探测半径r至少为多少海里?
(2)现有一艘敌舰A从东部接近△OBC海域,在某一时刻军舰B测得A位于北偏东60°方向上,同时军舰C测得A位于南偏东30°方向上,求此时敌舰A离△OBC海域的最短距离为多少海里?
(3)若敌舰A沿最短距离的路线以20
 海里/小时的速度靠近△OBC海域,我军军舰B沿北偏东15°的方向行进拦截,问B军舰速度至少为多少才能在此方向上拦截到敌舰A?
海里/小时的速度靠近△OBC海域,我军军舰B沿北偏东15°的方向行进拦截,问B军舰速度至少为多少才能在此方向上拦截到敌舰A?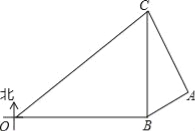
-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机小王某天下午营运的路线全是在东西走向的大道上,小王从点
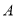 出发,如果规定向东为正,向西为负,他这天下午的行驶记录如下:+5,-3,-8,-6,+10,-6,+12,-10(单位:千米)
出发,如果规定向东为正,向西为负,他这天下午的行驶记录如下:+5,-3,-8,-6,+10,-6,+12,-10(单位:千米)(1)将最后一名乘客送到目的地时,小王距离出发点
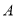 是多少千米?在点
是多少千米?在点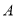 的哪个方向?
的哪个方向?(2)若汽车耗油量为
 升/千米,小王送完最后一个乘客后回到出发点
升/千米,小王送完最后一个乘客后回到出发点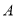 ,共耗油多少升?(用含
,共耗油多少升?(用含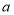 的代数式表示)
的代数式表示)(3)出租车油箱内原有12升油,请问:当
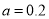 时,小王途中是否需要加油?若需要加油,至少需要加多少升油?如不需要,说明理由.
时,小王途中是否需要加油?若需要加油,至少需要加多少升油?如不需要,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点
 表示数
表示数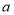 ,点
,点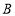 表示数
表示数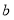 ,点
,点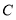 表示数
表示数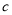 ,且点
,且点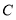 在点
在点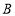 的左侧,同时
的左侧,同时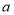 、
、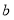 满足
满足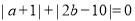 ,
,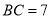 .
.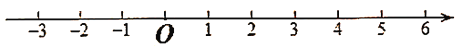
(1)由题意:
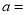 ______,
______,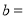 ______,
______,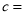 ______;
______;(2)当点
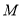 在数轴上运动时,点
在数轴上运动时,点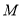 到
到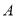 、
、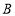 两点距离之和的最小值为______.
两点距离之和的最小值为______.(3)动点
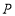 、
、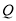 分别从点
分别从点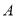 、
、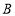 沿数轴负方向匀速运动同时出发,点
沿数轴负方向匀速运动同时出发,点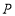 的速度是每秒
的速度是每秒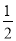 个单位长度,点
个单位长度,点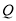 的速度是每秒2个单位长度,求运动几秒后,
的速度是每秒2个单位长度,求运动几秒后,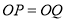 ?
?(4)在数轴上找一点
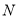 ,使点
,使点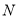 到
到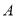 、
、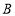 、
、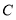 三点的距离之和等于10,请直接写出所有的点
三点的距离之和等于10,请直接写出所有的点 对应的数.(不必说明理由)
对应的数.(不必说明理由) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是AB的中点,点D是BC的中点,现给出下列等式:①CD=AC-DB,②CD=
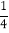 AB,③CD=AD-BC,④BD=2AD-AB.其中正确的等式编号是( )
AB,③CD=AD-BC,④BD=2AD-AB.其中正确的等式编号是( )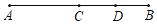
A.
 B.
B.  C.
C.  D.
D. 
相关试题

