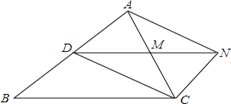
【题目】如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,若MA=MC.
(1)求证:CD=AN ;
(2)若AC⊥DN,∠CAN=30°,MN=1,求四边形ADCN的面积.
参考答案:
【答案】(1)证明:∵CN∥AB,∴∠DAC=∠NCA,即∠DAM=∠NCM。
在△AMD和△CMN中,∵∠DAM=∠NCM,MA="MC," ∠AMD∠CMN,
∴△AMD≌△CMN(ASA)。∴AD=CN,
又AD∥CN,∴四边形ADCN是平行四边形。
∴CD=AN。
(2)解:∵AC⊥DN,∠CAN=30°,MN=1,∴AN=2MN=2, 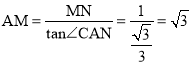 。
。
∴S△AMN![]() 。
。
∵四边形ADCN是平行四边形,
∴S四边形ADCN=4S△AMN=2![]() 。
。
【解析】试题分析:(1)利用“平行四边形ADCN的对边相等”的性质可以证得CD=AN;
(2)根据锐角三角函数定义求得AN=2MN=2, AM=![]() ,则S四边形ADCN=4S△AMN=2
,则S四边形ADCN=4S△AMN=2![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据3,1,5,1,3,4中,数据“3”出现的频数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:① AD∥BC;② ∠ACB=2∠ADB;③ ∠ADC=90°-∠ABD;④ BD平分∠ADC;⑤ 2∠BDC=∠BAC.其中正确的结论有 ( )
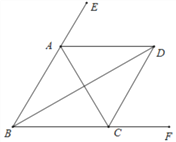
A. ①②④ B. ①③④⑤ C. ①②③⑤ D. ①②③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】我校学生会成员的年龄如下表:则出现频数最多的年龄是( )
年 龄
13
14
15
16
人数(人)
4
5
4
3
A.4
B.14
C.13和15
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】某市电力部门对居民用电按月收费,标准如下:
① 用电不超过100度的,每度收费0.5元;
② 用电超过100度的,超过部分每度收费0.8元.
(1)小明家1月份用电140度,应缴费________元;
(2)小华家2月份用电平均每度0.65元,问:他家2月份用了多少度电?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次数学测验后,张老师统计了全班50名同学的成绩,其中70分以下的占12%,70﹣80分的占24%,80﹣90分的占36%,请问90分及90分以上的有( )人.
A.13
B.14
C.15
D.28 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,点O是AC与BD的交点,过点O的直线与BA、DC的延长线分别交于点E、F.
求证:四边形AECF是平行四边形.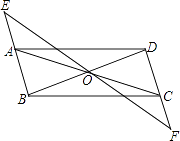
相关试题

