【题目】如图,已知在 ![]() 中,
中, ![]() ,
, ![]() 为
为 ![]() 边的中点,过点
边的中点,过点 ![]() 作
作 ![]() ,垂足分别为
,垂足分别为 ![]() .
.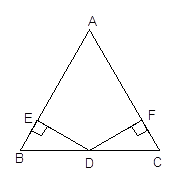
(1)求证: ![]() ;
;
(2)若 ![]() ,
, ![]() =
= ![]() ,求
,求 ![]() 的周长.
的周长.
参考答案:
【答案】
(1)证明: ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 是
是 ![]() 的中点,
的中点,
![]() .
.
![]() (AAS)
(AAS)
(2)解: ![]() ,
, ![]() ,
,
∴△ABC为等边三角形.
∴ ![]() ,
,
![]() ,
,
∴ ![]() ,
,
∴BE= ![]() BD,
BD,
![]() ,∴BD=2,∴BC=2BD=4,
,∴BD=2,∴BC=2BD=4,
∴ ![]() 的周长为12.
的周长为12.
【解析】(1)根据垂直的定义,可证得∠BED=∠CFD,再根据等边对等角去证明∠B=∠C ,根据线段中点的定义得出BD=CD,然后根据角角边证明△BED≌△CFD即可。
(2)根据有一个角是60°的等腰三角形是等边三角形,可证得△ABC为等边三角形,再根据30°角所对的直角边等于斜边的一半,求出BD的长,从而得到BC的长,即可求出△ABC的周长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0,
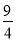 ),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.(1)求该抛物线的函数解析式;
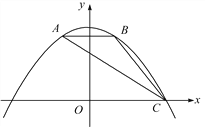
(2)点F为线段AC上一动点,过点F作FE⊥x轴,FG⊥y轴,垂足分别为点E,G,当四边形OEFG为正方形时,求出点F的坐标;
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算结果为a6的是( )
A.a2+a3
B.a2a3
C.(﹣a2)3
D.a8÷a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=
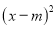 -(x-m),其中m是常数.
-(x-m),其中m是常数.(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;
(2)若该抛物线的对称轴为直线x=
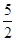
①求该抛物线的函数解析式;
②把该抛物线沿y轴向上平移多少个单位长度后,得到的抛物线与x轴只有一个公共点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,正确的有( )
A.a3+a2=a5B.2a3a2=2a6
C.(﹣2a3)2=4a6D.a8÷a2=a4
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年,某市发生了严重干旱,该市政府号召居民节约用水,为了解居民用水情况,在某小区随机抽查了10户家庭的月用水量,结果统计如图,则关于这10户家庭的月用水量,下列说法错误的是( )
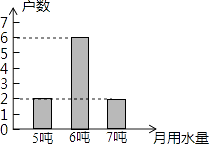
A.众数是6
B.中位数是6
C.平均数是6
D.方差是4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:

①FB⊥OC,OM=CM;
②△EOB≌△CMB;
③四边形EBFD是菱形;
④MB:OE=3:2.
其中正确结论的个数是( )
A.1
B.2
C.3
D.4
相关试题

