搜索
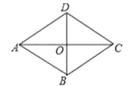
【题目】如图,平行四边形ABCD的两条对角线相交于O,且AC平分∠DAB
(1)求证:四边形ABCD是菱形
(2)若AC=16,BD=12,试求点O到AB的距离.
参考答案：
【答案】（1）证明见解析；（2）4.8
【解析】
(1)由平行四边形的对边平行得∠DAC=∠BCA，由角平分线的性质得∠DAC=∠BAC，即可知∠BCA=∠BAC，从而得AB=BC，即可得证；
(2)由菱形的对角线互相垂直且平分得AO=8、BO=6且∠AOB=90°，利用勾股定理得AB=10，根据S△AOB=
ABh=AOBO即可得答案．
(1)∵平行四边形ABCD，
∴AD//BC，
∴∠DAC=∠BCA，
∵AC平分∠DAB，
∴∠CAD=∠BAC，
∴∠ACB=∠BAC，
∴AB=BC，
∴ABCD是菱形；
(2)∵四边形ABCD是菱形，AC=16，BD=12，
所以AO=8，BO=6，
∵∠AOB=90°，
∴AB=
=10，
设O点到AB的距离为h，则
S△AOB=ABh=AOBO，
即：×10h=×8×6，
解得h=4.8，
所以O点到AB的距离为4.8.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连接PQ，BM，下面结论：
①△ABE≌△DBC；②∠DMA=60°；③△BPQ为等边三角形；④MB平分∠AMC，
其中结论正确的有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：∠ABC，∠ACB的平分线相交于F点，过点F作DE∥BC，交AB于点D，交AC于点E．
（1）请你写出图中所有的等腰三角形；
（2）请写出BD，CE，DE之间的数量关系；
（3）并对第（2）问中BD，CE，DE之间的数量关系给予证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】全民健身运动已成为一种时尚，为了了解我市居民健身运动的情况，某健身馆的工作人员开展了一项问卷调查，问卷包括五个项目：A：健身房运动；B：跳广场舞；C：参加暴走团；D：散布；E：不运动．
以下是根据调查结果绘制的统计图表的一部分．
运动形式
A
B
C
D
E
人数
12
30
m
54
9
请你根据以上信息，回答下列问题：
（1）接受问卷调查的共有 人，图表中的m= ，n= ；
（2）统计图中，A类所对应的扇形圆心角的度数为 ；
（3）根据调查结果，我市市民最喜爱的运动方式是 ，不运动的市民所占的百分比是 ；
（4）我市碧沙岗公园是附近市民喜爱的运动场所之一，每晚都有“暴走团”活动，若最邻近的某社区约有1500人，那么估计一下该社区参加碧沙岗“暴走团”的大约有多少人？
-
科目： 来源： 题型：
查看答案和解析>>【题目】八年级380名师生参加户外拓展活动,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表
甲种客车
乙种客车
载客量（座/辆）
60
45
租金（元/辆）
550
450
(1)设租用乙种客车x辆,租车总费用为y元求出y(元)与x(辆)之间的函数表达式;
(2)当乙种客车租用多少辆时,能保障所有的师生能参加户外拓展活动且租车费用最少，最少费用是多少元?
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=kx-3与x轴、y轴分别相交于B、C两点，且OC=2OB
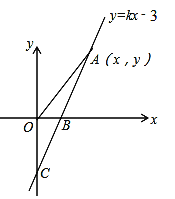
（1）求B点的坐标和k的值.
（2）若点A（x,y）是直线y=kx-3上在第一象限内的一个动点，当A 在运动的过程中，试写出△AOB的面积S与x的函数关系式，（不要求写出自变量的取值范围）.
（3）探究：在（2）的条件下
①当A运动到什么位置时，△ABO的面积为
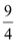，并说明理由.②在①成立的情况下，x轴上是否存在一点P，使△AOP是等腰三角形？若存在，请直接写出满足条件的所有P点的坐标，若不存在，请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在等腰Rt△ABC中，∠ACB＝90°，AC＝CB，F是AB边上的中点，点D、E分别在AC、BC边上运动，且始终保持AD＝CE．连接DE、DF、EF．
（1）求证：△ADF≌△CEF；
（2）试证明△DFE是等腰直角三角形．
相关试题
