【题目】在平面直角坐标系中,点A(a ,2![]() )是直线y=
)是直线y=![]() x上一点,以A为圆心,2为半径作⊙A,若P(x,y)是第一象限内⊙A上任意一点,则
x上一点,以A为圆心,2为半径作⊙A,若P(x,y)是第一象限内⊙A上任意一点,则![]() 的最小值为( )
的最小值为( )
A. 1 B. ![]() C.
C. ![]() —1 D.
—1 D. ![]()
参考答案:
【答案】D
【解析】分析: 如图所示,当直线OP与圆A相切时,连接AP,过P作PH⊥x轴,此时![]() 取得最小值,利用切线的性质得到AP垂直于OP,在直角三角形AOP中,根据到角两边距离相等的点在角的平分线上确定出∠AOP=30°,
取得最小值,利用切线的性质得到AP垂直于OP,在直角三角形AOP中,根据到角两边距离相等的点在角的平分线上确定出∠AOP=30°,![]() 为tan∠30°的值,求出即可.
为tan∠30°的值,求出即可.
详解: 如图所示,当直线OP与圆A相切时,连接AP,过P作PH⊥x轴,此时![]() 取得最大值,
取得最大值,
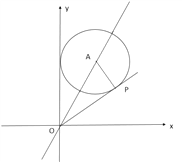
∵点A(a ,2![]() )是直线y=
)是直线y=![]() x上一点,
x上一点,
∴a=2,
∴A(2 ,2![]() ).
).
∵以A为圆心,2为半径作⊙A,
∴⊙A与y轴相切.
则当直线OP与圆A相切时, ![]() 取得最小值,
取得最小值,
∵∠AOy=∠AOP=30°,
∴∠AOx=30°,
∴此时![]() =tan30°=
=tan30°=![]() ,
,
则![]() 的最小值为
的最小值为![]() .
.
故选:D.
点睛:
此题考查了切线的性质,坐标与图形性质,以及锐角三角函数定义,熟练掌握切线的性质是解本题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为绿化校园,安排七年级三个班植树,其中,一班植树x棵,二班植树的棵数是一班的2倍少20棵,三班植树的棵数是二班的一半多15棵.
(1)三个班共植树多少棵?(用含x的式子表示)
(2)当x=30时,三个班中哪个班植树最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,既是中心对称图形又是轴对称图形的是( )

A. (A) B. (B) C. (C) D. (D)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验,它们的平均亩产量分别是
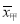 =610千克,
=610千克, 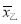 =609千克,亩产量的方差分别是
=609千克,亩产量的方差分别是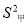 =29.6,
=29.6, 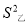 =2.则关于两种小麦推广种植的合理决策是( )
=2.则关于两种小麦推广种植的合理决策是( )A. 甲的平均亩产量较高,应推广甲
B. 甲、乙的平均亩产量相差不多,均可推广
C. 甲的平均亩产量较高,且亩产量比较稳定,应推广甲
D. 甲、乙的平均亩产量相差不多,但乙的亩产量比较稳定,应推广乙
-
科目: 来源: 题型:
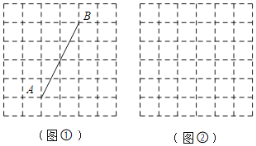
查看答案和解析>>【题目】如图,正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫格点.
(1)在图①中,线段AB的长度为 ;若在图中画出以C为直角顶点的Rt△ABC,使点C在格点上,请在图中画出所有点C;
(2)在图②中,以格点为顶点,请先用无刻度的直尺画正方形ABCD,使它的面积为13;再画一条直线PQ(不与正方形对角线重合),使PQ恰好将正方形ABCD的面积二等分(保留作图痕迹).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂为了解甲、乙两个部门员工的生产技能情况,从甲、乙两个部门各随机抽取20名员工,进行生产技能测试,测试成绩(百分制)如下:
甲7886 748175768770759075798170748086698377
乙9373 888172819483778380817081737882807040
(说明:成绩80分及以上为优秀,70-79分为良好,60-69分为合格,60分以下为不合格)
(1)请填完整表格:
部门
平均数
中位数
众数
甲
78.3
75
乙
78
80.5
(2)从样本数据可以推断出 部门员工的生产技能水平较高,请说明理由.(至少从两个不同的角度说明推断的合理性).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形纸片ABCD的边长为2,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P、EF、GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:①当x=1时,点P是正方形ABCD的中心;②当x=
 时,EF+GH>AC;③当0<x<2时,六边形AEFCHG面积的最大值是3;④当0<x<2时,六边形AEFCHG周长的值不变.其中正确的选项是( )
时,EF+GH>AC;③当0<x<2时,六边形AEFCHG面积的最大值是3;④当0<x<2时,六边形AEFCHG周长的值不变.其中正确的选项是( )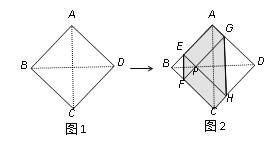
A. ①③ B. ①②④ C. ①③④ D. ①②③④
相关试题

