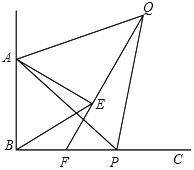
【题目】如图,![]() ,P为射线BC上任意一点
,P为射线BC上任意一点![]() 点P和点B不重合
点P和点B不重合![]() ,分别以AB,AP为边在
,分别以AB,AP为边在![]() 内部作等边
内部作等边![]() 和等边
和等边![]() ,连结QE并延长交BP于点F,连接EP,若
,连结QE并延长交BP于点F,连接EP,若![]() ,
,![]() ,则
,则![]() ______.
______.
参考答案:
【答案】![]()
【解析】
连接EP,过点E作![]() ,由题意可得△AQE≌△ABP,可得QE=BP,
,由题意可得△AQE≌△ABP,可得QE=BP,![]() ,可求
,可求![]() ,根据勾股定理可求
,根据勾股定理可求![]() , BM=
, BM=![]() EM,EF=BF=2FM,EM=
EM,EF=BF=2FM,EM=![]() FM,可求BF=EF=4,EM=2
FM,可求BF=EF=4,EM=2![]() ,FM=2,由QF=11,EF=4,可得BP=EQ=7,可求MP的长,根据勾股定理可求EP的长.
,FM=2,由QF=11,EF=4,可得BP=EQ=7,可求MP的长,根据勾股定理可求EP的长.
解:如图:连接EP,过点E作![]() .
.
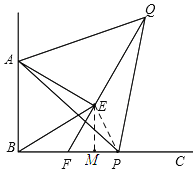
∵△AEB,△APQ是等边三角形
∴ AB=AE=BE=4![]() ,AQ=AP,∠ABE=∠BAE=∠QAP=60°=∠AEB,
,AQ=AP,∠ABE=∠BAE=∠QAP=60°=∠AEB,
∴∠BAP=∠EAQ,且AP=AQ,AB=AE,
∴ △ABP≌△AEQ,
∴EQ=BP,∠AEQ=∠ABC=90°,
∴∠BEF=∠EBF=30°,
∴BF=EF,∠EFM=60°,
∵![]() ,
,
∴∠FEM=30°,
∴EF=2FM =BF,EM=![]() FM,
FM,
∵∠EBM=30°,![]() ,
,
∴BE=2EM,BM=![]() EM,
EM,
∵EB=4![]() ,
,
∴EM=2![]() ,BM=6,
,BM=6,
∵BF+FM=BM,
∴FM=2,BF=EF=4,
∵QF=EF+EF,
∴EQ=11-4=7,
∴ BP=7,
∴MP=BP –BM =1,
在Rt△EMP中,![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在综合与实践课上,同学们以“一个含
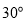 的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线
的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线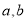 且
且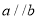 和直角三角形
和直角三角形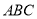 ,
,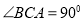 ,
,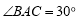 ,
,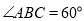 .
.操作发现:
(1)在如图1中,
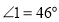 ,求
,求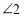 的度数;
的度数;(2)如图2,创新小组的同学把直线
 向上平移,并把
向上平移,并把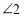 的位置改变,发现
的位置改变,发现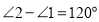 ,说明理由;
,说明理由;实践探究:
(3)缜密小组在创新小组发现结论的基础上,将如图中的图形继续变化得到如图,
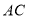 平分
平分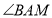 ,此时发现
,此时发现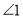 与
与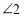 又存在新的数量关系,请直接写出
又存在新的数量关系,请直接写出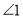 与
与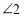 的数量关系.
的数量关系.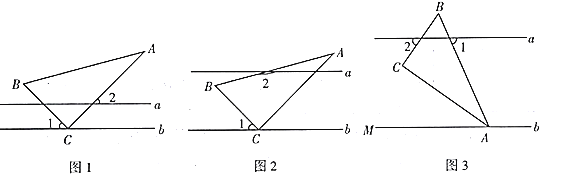
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形纸片ABCD的边长为3,点E,F分别在边BC、CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( )

A.1.5
B.2.5
C.2.25
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
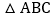 中,
中,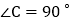 ,
,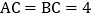 ,D是AB的中点,点E、F分别在AC、BC边上运动
,D是AB的中点,点E、F分别在AC、BC边上运动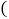 点E不与点A、C重合
点E不与点A、C重合 ,且保持
,且保持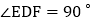 ,连接DE、DF、
,连接DE、DF、 在此运动变化的过程中,有下列结论:
在此运动变化的过程中,有下列结论: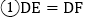 ;
; 四边形CEDF的面积随点E、F位置的改变而发生变化;
四边形CEDF的面积随点E、F位置的改变而发生变化;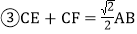 ;
;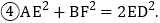 以上结论正确的是______
以上结论正确的是______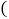 只填序号
只填序号 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
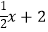 与y轴交于点A,与直线y=﹣
与y轴交于点A,与直线y=﹣ 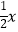 交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x﹣h)2+k的顶点在直线y=﹣
交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x﹣h)2+k的顶点在直线y=﹣ 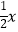 上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
A.﹣2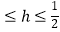
B.﹣2≤h≤1
C.﹣1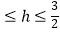
D.﹣1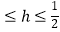
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,已知点
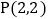 ,C为y轴正半轴上一点,连接PC,线段PC绕点P顺时针旋转
,C为y轴正半轴上一点,连接PC,线段PC绕点P顺时针旋转 至线段PD,过点D作直线
至线段PD,过点D作直线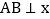 轴,垂足为B,直线AB与直线OP交于点A,且
轴,垂足为B,直线AB与直线OP交于点A,且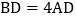 ,直线CD与直线OP交于点Q,则点Q的坐标为______.
,直线CD与直线OP交于点Q,则点Q的坐标为______.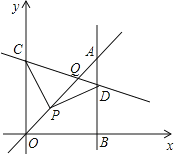
-
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接广州市青少年读书活动,某校倡议同学们利于课余时间多阅读为了解同学们的读书情况,在全校随机调查了部分同学在一周内的阅读时间,并用得到的数据绘制了统计图,根据图中信息解答下列问题:
 被抽查学生阅读时间的中位数为多少小时,众数为多少小时,平均数为多少小时;
被抽查学生阅读时间的中位数为多少小时,众数为多少小时,平均数为多少小时; 已知全校学生人数为1500人,请你估算该校学生一周内阅读时间不少于三小时的有多少人?
已知全校学生人数为1500人,请你估算该校学生一周内阅读时间不少于三小时的有多少人?
相关试题

