搜索
【题目】一个多边形的内角和是它外角和的1.5倍，那么这个多边形是______边形．
参考答案：
【答案】五
【解析】
设多边形边数为n.
则360°×1.5=(n2)180°，
解得n=5.
故选C.
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列四组线段中，能组成直角三角形的是（ ）
A. a＝2，b＝4，c＝6B. a＝4，b＝6，c＝8
C. a＝4，b＝8，c＝10D. a＝6，b＝8，c＝10
-
科目： 来源： 题型：
查看答案和解析>>【题目】某旅行社组团去外地旅游，30人起组团，每人单价800元．旅行社对超过30人的团给予优惠，即旅行团的人数每增加一人，每人的单价就降低10元．当一个旅行团的人数是______人时，这个旅行社可以获得最大的营业额．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平行四边形ABCD中，对角线AC与BD相交于点O，AC＝12，BD＝10，AB＝m，那么m的取值范围是（ ）
A. 5＜m＜6B. 1＜m＜11C. 10＜m＜12D. 10＜m＜22
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，抛物线C：y=ax2．
（1）若直线l1：y=x-1与抛物线C有且只有1个交点，求抛物线C的解析式．
（2）如图1，在（1）的条件下，在y轴上有一点A（0，4），过点A作直线l2与抛物线C有两个交点M、N（N位于第一象限），过点N作x轴的垂线，垂足为H．试探究：是否存在l2，使△MON∽△NHO？若存在，求出l2的解析式；若不存在，说明理由．
（3）如图2，E、F为抛物线C（y=ax2）上两动点，始终满足OE⊥OF，连接EF，则直线EF是否恒过一定点G？若存在点G，直接写出G点坐标（用含a的坐标表示），若不存在，给予证明．
（参考结论：若直线l：y=kx+b上有两点（x1，y1）、（x2，y2），则斜率k=
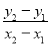；当两直线l1、l2的斜率乘积k1k2=-1时，l1⊥l2）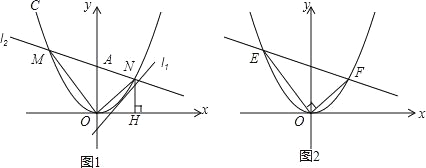
-
科目： 来源： 题型：
查看答案和解析>>【题目】抛物线y＝(x－1)2＋1的顶点坐标为( )
A. (1，1) B. (1，－1)
C. (－1，1) D. (－1，－1)
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个三角形一条边长为a＋b，另一条边比这条边长2a＋b，第三条边比这条边短3a－b，则这个三角形的周长为____________．
相关试题
