【题目】某中学计划从办公用品公司购买A,B两种型号的小黑板.经洽谈,购买一块A型小黑板比购买一块B型小黑板多用20元,且购买5块A型小黑板和4块B型小黑板共需820元.
(1)求购买一块A型小黑板、一块B型小黑板各需多少元.
(2)根据该中学实际情况,需从公司购买A,B两种型号的小黑板共60块,要求购买A,B两种型号小黑板的总费用不超过5240元.并且购买A型小黑板的数量不小于购买B型小黑板数量的 ![]() .则该中学从公司购买A,B两种型号的小黑板有哪几种方案?哪种方案的总费用最低?
.则该中学从公司购买A,B两种型号的小黑板有哪几种方案?哪种方案的总费用最低?
参考答案:
【答案】
(1)解:设一块A型小黑板x元,一块B型小黑板y元.
则 ![]() ,
,
解得 ![]() .
.
答:一块A型小黑板100元,一块B型小黑板80元
(2)解:设购买A型小黑板m块,则购买B型小黑板(60﹣m)块
则 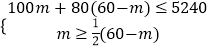 ,
,
解得20≤m≤22,
又∵m为正整数
∴m=20,21,22
则相应的60﹣m=40,39,38
∴共有三种购买方案,分别是
方案一:购买A型小黑板20块,购买B型小黑板40块;
方案二:购买A型小黑板21块,购买B型小黑板39块;
方案三:购买A型小黑板22块,购买B型小黑板38块.
方案一费用为100×20+80×40=5200元;
方案二费用为100×21+80×39=5220元;
方案三费用为100×22+80×38=5240元.
∴方案一的总费用最低,
即购买A型小黑板20块,购买B型小黑板40块总费用最低,为5200元
【解析】(1)设购买一块A型小黑板需要x元,一块B型为y元,根据等量关系:购买一块A型小黑板比买一块B型小黑板多用20元;购买5块A型小黑板和4块B型小黑板共需820元;可列方程组求解.(2)设购买A型小黑板m块,则购买B型小黑板(60﹣m)块,根据需从公司购买A、B两种型号的小黑板共60块,要求购买A、B两种型号小黑板的总费用不超过5240元.并且购买A型小黑板的数量不小于购买B型小黑板数量的 ![]() ,可列不等式组求解.
,可列不等式组求解.
【考点精析】关于本题考查的一元一次不等式组的应用,需要了解1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(﹣1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.
(1)若抛物线经过点C、A、A′,求此抛物线的解析式;
(2)点M时第一象限内抛物线上的一动点,问:当点M在何处时,△AMA′的面积最大?最大面积是多少?并求出此时M的坐标;
(3)若P为抛物线上一动点,N为x轴上的一动点,点Q坐标为(1,0),当P、N、B、Q构成平行四边形时,求点P的坐标,当这个平行四边形为矩形时,求点N的坐标.


-
科目: 来源: 题型:
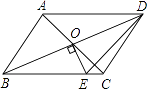
查看答案和解析>>【题目】如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为10,则平行四边形ABCD的周长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组
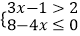 的解集在数轴上表示为( )
的解集在数轴上表示为( )
A.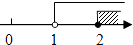
B.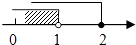
C.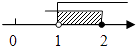
D.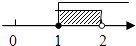
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF交于点G.
(1)如图①,若四边形ABCD是矩形,且DE⊥CF.求证:
 ;
;(2)如图②,若四边形ABCD是平行四边形.试探究:当∠B与∠EGC满足什么关系时,使得
 成立?并证明你的结论;
成立?并证明你的结论;(3)如图③,若BA=BC=9,DA=DC=12,∠BAD=90°,DE⊥CF.求出
 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】林老师骑摩托车到加油站加油,发现每个加油器上都有三个量,其中一个表示“元/升”其数值固定不变的,另外两个量分别表示“数量”、“金额”,数值一直在变化,在这三个量当中是常量,是变量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a=﹣(0.3)2 , b=﹣3﹣2 , c=(﹣
 )﹣2 , d=(﹣
)﹣2 , d=(﹣  )0 , 用“<”连接a、b、c、d为 .
)0 , 用“<”连接a、b、c、d为 .
相关试题

