【题目】已知Rt△ABC的斜边AB在平面直角坐标系的x轴上,点C(1,3)在反比例函数y=![]() 的图象上,且sin∠BAC=
的图象上,且sin∠BAC=![]() .
.
(1)求k的值和边AC的长;
(2)求点B的坐标.
参考答案:
【答案】(1) k的值和边AC的长分别是:3,5.(2) 点B的坐标是(-![]() ,0),(
,0),(![]() ,0).
,0).
【解析】
试题分析:(1)本题需先根据C点的坐标在反比例函数y=![]() 的图象上,从而得出k的值,再根据且sin∠BAC=
的图象上,从而得出k的值,再根据且sin∠BAC=![]() ,得出AC的长.
,得出AC的长.
(2)本题需先根据已知条件,得出∠DAC=∠DCB,从而得出CD的长,根据点B的位置即可求出正确答案.
试题解析:(1)∵点C(1,3)在反比例函数y=![]() 的图象上,
的图象上,
∴3=![]() ,解得k=3,
,解得k=3,
∵sin∠BAC=![]()
∴sin∠BAC=![]() =
=![]()
∴AC=5;
∴k的值和边AC的长分别是:3,5.
(2)①当点B在点A右边时,如图,
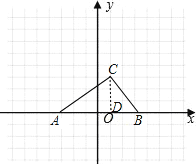
作CD⊥x轴于D.
∵△ABC是直角三角形,
∴∠DAC=∠DCB,
又∵sin∠BAC=![]() ,
,
∴tan∠DAC=![]() ,
,
∴![]() ,
,
又∵CD=3,
∴BD=![]() ,
,
∴OB=1+![]() =
=![]() ,
,
∴B(![]() ,0);
,0);
②当点B在点A左边时,如图,
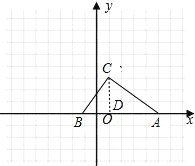
作CD⊥x轴于D.
∵△ABC是直角三角形,
∴∠B+∠A=90°,∠B+∠BCD=90°,
∴∠DAC=∠DCB,
又∵sin∠BAC=![]() ,
,
∴tan∠DAC=![]() ,
,
∴![]() ,
,
又∵CD=3,
∴BD=![]() ,BO=BD-1=
,BO=BD-1=![]() ,
,
∴B(-![]() ,0)
,0)
∴点B的坐标是(-![]() ,0),(
,0),(![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】请将下面的说理过程和理由补充完整.
已知:如图,AB∥CD,∠B=∠D,说明:BF∥DE.

解:AB∥CD.(已知)
∴∠A=∠C.( ____①___)
在△ABF和△CDE中
∵∠B=∠D=90°,(已知)
∴∠A+∠AFB=90°
∠C+___②___=90°.(直角三角形的两个锐角互余)
又∵∠A=∠C,(已证).
∴∠AFB=____③_____.(_____④_____)
∴BF∥DE.( ___⑤_____)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发生了求救信号,一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里/时的速度前往救援,求海警船到达事故船C处所需的大约时间.(参考数据:sin53°≈0.8,cos53°≈0.6)

-
科目: 来源: 题型:
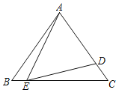
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=6,点D在边AC上,AD的中垂线交BC于点E.若∠AED=∠B,CE=3BE,则CD等于( )
A.
 B. 2C.
B. 2C.  D. 3
D. 3 -
科目: 来源: 题型:
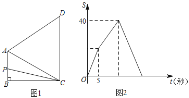
查看答案和解析>>【题目】如图1,四边形ABCD中,AB∥CD,∠B=90°,AC=AD.动点P从点B出发沿折线B-A-D-C方向以1单位/秒的速度运动,在整个运动过程中,△BCP的面积S与运动时间t(秒)的函数图象如图2所示,则AD等于( )
A. 10B.
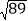 C. 8D.
C. 8D. 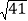
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠ACB与∠CAB的平分线交于点P,PD⊥AB于点D,若△APC与△APD的周长差为
 ,四边形BCPD的周长为12+
,四边形BCPD的周长为12+ ,则BC等于______.
,则BC等于______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是小章为学校举办的数学文化节没计的标志,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI上,若AC+BC=6,空自部分面积为10.5,则阴影部分面积为______.

相关试题

