【题目】某手机经销商计划同时购进一批甲、乙两种型号手机,若购进2部甲型号手机和5部乙型号手机,共需要资金6000元;若购进3部甲型手机和2部乙型手机,共需要资金4600元.
(1) 求甲、乙型号手机每部进价为多少元?
(2) 为了提高利润,该店计划购进甲、乙型号手机销售,预计用不多于1.84万元且不少于1.76万元的资金购进这两种手机共20部,请问有几种进货方案?
参考答案:
【答案】(1)购进一部甲型手机和一部乙型手机分别为1000元,800元;(2)即共有3种方案: 购进甲 8部,购进乙12部;购进甲9部,购进乙 11部;购进甲10部,购进乙 10部.
【解析】
(1)设购进一部甲型手机和一部乙型手机分别为x元、y元,根据题中的两个等量关系:①购买2部甲型手机的费用+购买5部乙型手机的费用=6000;②购买3部甲型手机的费用+购买2部乙型手机的费用=4600列出方程组,解方程组即可求得本题答案;
(2)设购进甲型手机a部,则购进乙型手机(20-a)部,结合(1)中所得两种型号手机的单价,表示出购买这些手机所需的总费用,结合题中已知条件:总费用不超过1.84万元和不少于1.76万元列出不等式组,解不等式组求得整数解即可得到所求进货方案;
(1)设购进一部甲型手机和一部乙型手机分别需要x元、y元, 根据题意得:
![]() ,
,
解方程组得:![]() ,
,
答:购进一部甲型手机和一部乙型手机分别需要1000元,800元.
(2)设购进甲型手机a部,则购进乙型手机(180-a)部,根据题意得:
![]() ,
,
解不等式组得:![]() ,
,
∵a只能取整数,
∴![]() =8,9或10 ;
=8,9或10 ;
即共有3种方案: ①购进甲 8部,乙12部;②购进甲9部,乙 11部;③购进甲 10部,乙 10部.
-
科目: 来源: 题型:
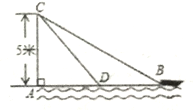
查看答案和解析>>【题目】在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13m,此人以0.5m/s的速度收绳.10s后船移动到点D的位置,问船向岸边移动了多少m?(假设绳子是直的,结果保留根号)
-
科目: 来源: 题型:
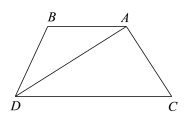
查看答案和解析>>【题目】如图,已知AB∥CD,AD平分∠BDC.
(1)求证:∠BAD=∠BDA;
(2)若AD⊥AC,∠C=700,求∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解同学对体育活动的喜爱情况,某校设计了“你最喜欢的体育活动是哪一项(仅限一项)”的调查问卷.该校对本校学生进行随机抽样调查,以下是根据调查数据得到的统计图的一部分.请根据以上信息解答以下问题:
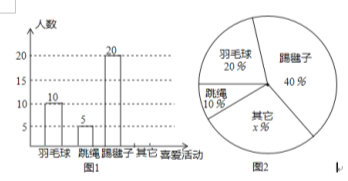
(1)该校对多少名学生进行了抽样调查?
(2)①请补全图1并标上数据 ②图2中x= .
(3)若该校共有学生900人,请你估计该校最喜欢跳绳项目的学生约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果一个数的平方等于
 ,记为
,记为 ,这个数
,这个数 叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为
叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为 (
( 、
、 为实数),
为实数), 叫这个复数的实部,
叫这个复数的实部,  叫做这个复数的虚部,它的加、减、乘法运算与整式的加、减、乘法运算类似.
叫做这个复数的虚部,它的加、减、乘法运算与整式的加、减、乘法运算类似.例如计算:
 .
.(
 )填空:
)填空: 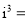 __________,
__________,  __________;
__________;(
 )计算:
)计算:  ;
;(
 )试一试:请利用近期学习的有关知识和方法将
)试一试:请利用近期学习的有关知识和方法将 化简成
化简成 的形式.
的形式. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋里装有红、黑、绿三种颜色的乒乓球(除颜色外其余都相同),其中红球有2个,黑球有1个,绿球有3个,第一次任意摸出一个球(不放回),第二次再摸出一个球,则两次摸到的都是红球的概率为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为
 的中点,D、E分别是OA、OB的中点,则图中阴影部分的面积为cm2 .
的中点,D、E分别是OA、OB的中点,则图中阴影部分的面积为cm2 . 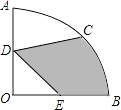
相关试题

