【题目】如图,直线y= ![]() x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).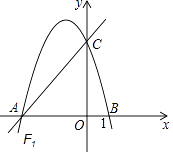
(1)求抛物线F1所表示的二次函数的表达式及顶点Q的坐标;
(2)在抛物线上是否存在点P,使△BPC的内心在y轴上,若存在,求出点P的坐标,若不存在写出理由;
(3)直线y=kx﹣6与y轴交于点N,与直线AC的交点为M,当△MNC与△AOC相似时,求点M坐标.
参考答案:
【答案】
(1)解:令y=0代入y= ![]() x+4,解得:x=﹣3,
x+4,解得:x=﹣3,
∴A(﹣3,0).
令x=0,代入y= ![]() x+4,得y=4,
x+4,得y=4,
∴C(0,4).
设抛物线F1的解析式为:y=a(x+3)(x﹣1),
把C(0,4)代入上式得,a=﹣ ![]() ,
,
∴y=﹣ ![]() x2﹣
x2﹣ ![]() x+4.
x+4.
∴y=﹣ ![]() (x2+2x+1)+
(x2+2x+1)+ ![]() ,
,
∴Q(﹣1, ![]() ).
).
(2)解:∵点B的坐标为(1,0),取点B关于y轴的对称点B′(﹣1,0),连接CB′,则∠BCO=∠B′CO,
∴△BPC的内心在y轴上.
设直线B′C的解析式为y=kx+b,将点B′和点C的坐标代入得: ![]() ,
,
解得:k=4,b=4.
∴直线B′C的解析式为y=4x+4,
将y=4x+4与y=﹣ ![]() x2﹣
x2﹣ ![]() x+4联立得:
x+4联立得: 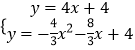 ,
,
解得: ![]() 或
或 ![]() (舍去).
(舍去).
∴点P的坐标为(﹣5,﹣16)
(3)解:N(0,﹣6),直线AC的表达式为y= ![]() x+4.
x+4.
当△MNC∽△AOC时,∠CMN=90°.
∴直线MN的一次项系数为﹣ ![]() .
.
∴MN的解析式为y=﹣ ![]() x﹣6.
x﹣6.
将y= ![]() x+4与y=﹣
x+4与y=﹣ ![]() x﹣6联立,解得:
x﹣6联立,解得: 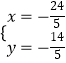 ,
,
∴点M的坐标为(﹣ ![]() ,﹣
,﹣ ![]() ).
).
②当∠CNM为直角时,MN∥x轴,
将y=﹣6代入y= ![]() x+4得:
x+4得: ![]() x+4=﹣6,解得:x=﹣
x+4=﹣6,解得:x=﹣ ![]() .
.
∴M(﹣ ![]() ,﹣6).
,﹣6).
综上所述,点M的坐标为(﹣ ![]() ,﹣
,﹣ ![]() )或(﹣
)或(﹣ ![]() ,﹣6)
,﹣6)
【解析】(1)先求得点A和点C的坐标,然后利用待定系数法求得二次函数的额解析式,接下来,利用配方法求得抛物线的顶点坐标即可;
(2)取点B关于y轴的对称点B′(-1,0),连接CB′,则∠BCO=∠B′CO,然后求得直线B′C的解析式为,然后将直线B′C的解析式与抛物线的解析式联立可求得点P的坐标;
(3)当∠CMN=90°时,先求得直线MN的解析式,然后将直线AC与直线MN的解析式联立可求得点点M的坐标;当∠CNM为直角时,MN∥x轴,再求得直线MN的解析式,然后将直线AC与直线MN的解析式联立可求得点点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.
求证:AF平分∠BAC.

【答案】证明见解析.
【解析】试题分析:先根据AB=AC,可得∠ABC=∠ACB,再由垂直,可得90°的角,在△BCE和△BCD中,利用内角和为180°,可分别求∠BCE和∠DBC,利用等量减等量差相等,可得FB=FC,再易证△ABF≌△ACF,从而证出AF平分∠BAC.
试题解析:证明:∵AB=AC(已知),
∴∠ABC=∠ACB(等边对等角).
∵BD、CE分别是高,
∴BD⊥AC,CE⊥AB(高的定义).
∴∠CEB=∠BDC=90°.
∴∠ECB=90°∠ABC,∠DBC=90°∠ACB.
∴∠ECB=∠DBC(等量代换).
∴FB=FC(等角对等边),
在△ABF和△ACF中,
 ,
,∴△ABF≌△ACF(SSS),
∴∠BAF=∠CAF(全等三角形对应角相等),
∴AF平分∠BAC.
【题型】解答题
【结束】
23【题目】如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.

(1)求证:CD=BE;
(2)已知CD=2,求AC的长;
(3)求证:AB=AC+CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=_____.
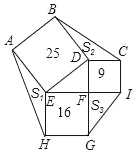
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD中,两条对角线AC,BD相交于点O,∠MON+∠BCD=180°,∠MON绕点O旋转,射线OM交边BC于点E,射线ON交边DC于点F,连接EF.
(1)如图1,当∠ABC=90°时,△OEF的形状是;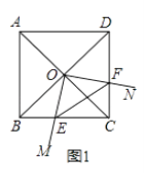
(2)如图2,当∠ABC=60°时,请判断△OEF的形状,并说明理由;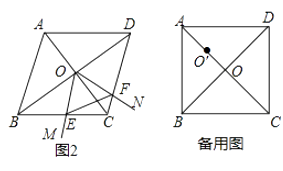
(3)在(1)的条件下,将∠MON的顶点移到AO的中点O′处,∠MO′N绕点O′旋转,仍满足∠MO′N+∠BCD=180°,射线O′M交直线BC于点E,射线O′N交直线CD于点F,当BC=4,且 =
=  时,直接写出线段CE的长.
时,直接写出线段CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读与理解:
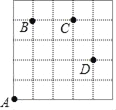
如图,一只甲虫在5×5的方格(每个方格边长均为1)上沿着网格线爬行.若我们规定:在如图网格中,向上(或向右) 爬行记为“+”,向下(或向左) 爬行记为“﹣”,并且第一个数表示左右方向,第二个数表示上下方向.
例如:从A到B记为:A→B(+1,+4),从D到C记为:D→C(﹣1,+2).
思考与应用:
(1)图中A→C( , ),B→C( , ),D→A( , )
(2)若甲虫从A到P的行走路线依次为:(+3,+2)→(+1,+3)→(+1,﹣2),请在图中标出P的位置.
(3)若甲虫的行走路线为A→(+1,+4)→(+2,0)→(+1,﹣2)→(﹣4,﹣2),请计算该甲虫走过的总路程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF=( )
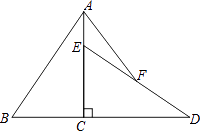
A.4
B.5
C.4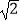
D.6 -
科目: 来源: 题型:
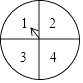
查看答案和解析>>【题目】如图,转盘被划分成4个相同的小扇形,并分别标上数字1,2,3,4,分别转动两次转盘,转盘停止后,指针所指向的数字作为直角坐标系中M点的坐标(第一次作横坐标,第二次作纵坐标),指针如果指向分界线上,认为指向左侧扇形的数字,则点M落在直线y=x的下方的概率为( )
A.
B.
C.
D.
相关试题

