【题目】我们定义:如图1,在![]() 中,把AB绕点A顺时针旋转
中,把AB绕点A顺时针旋转![]() 得到
得到![]() ,把AC绕点A逆时针旋转
,把AC绕点A逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() 当
当![]() 时,我们称
时,我们称![]() 是
是![]() 的“旋补三角形”,
的“旋补三角形”, ![]() 边
边![]() 上的中线AD叫做
上的中线AD叫做![]() 的“旋补中线”,点A叫做“旋补中心”.
的“旋补中线”,点A叫做“旋补中心”.
特例感知:
![]() 在图2,图3中,
在图2,图3中,![]() 是
是![]() 的“旋补三角形”,AD是
的“旋补三角形”,AD是![]() 的“旋补中线”.
的“旋补中线”.
![]() 如图2,当
如图2,当![]() 为等边三角形时,AD与BC的数量关系为
为等边三角形时,AD与BC的数量关系为![]() ______BC;
______BC;
![]() 如图3,当
如图3,当![]() ,
,![]() 时,则AD长为______.
时,则AD长为______.
猜想论证:
![]() 在图1中,当
在图1中,当![]() 为任意三角形时,猜想AD与BC的数量关系,并给予证明.
为任意三角形时,猜想AD与BC的数量关系,并给予证明.
拓展应用
![]() 如图4,在四边形ABCD,
如图4,在四边形ABCD,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 在四边形内部是否存在点P,使
在四边形内部是否存在点P,使![]() 是
是![]() 的“旋补三角形”?若存在,给予证明,并求
的“旋补三角形”?若存在,给予证明,并求![]() 的“旋补中线”长;若不存在,说明理由.
的“旋补中线”长;若不存在,说明理由.

参考答案:
【答案】(1)①![]() ;②4;(2)结论:
;②4;(2)结论:![]() .详见解析;(3)
.详见解析;(3)![]() 的“旋补中线”长
的“旋补中线”长![]() .
.
【解析】
(1)①首先证明![]() 是含有
是含有![]() 是直角三角形,可得
是直角三角形,可得![]() 即可解决问题;②首先证明
即可解决问题;②首先证明![]() ≌
≌![]() ,根据直角三角形斜边中线定理即可解决问题;(2)结论:
,根据直角三角形斜边中线定理即可解决问题;(2)结论:![]() 如图1中,延长AD到M,使得
如图1中,延长AD到M,使得![]() ,连接
,连接![]() ,
,![]() ,首先证明四边形
,首先证明四边形![]() 是平行四边形,再证明
是平行四边形,再证明![]() ≌
≌![]() ,即可解决问题;(3)存在
,即可解决问题;(3)存在![]() 如图4中,延长AD交BC的延长线于M,作
如图4中,延长AD交BC的延长线于M,作![]() 于E,作线段BC的垂直平分线交BE于P,交BC于F,连接PA、PD、PC,作
于E,作线段BC的垂直平分线交BE于P,交BC于F,连接PA、PD、PC,作![]() 的中线
的中线![]() 连接DF交PC于
连接DF交PC于![]() 想办法证明
想办法证明![]() ,
,![]() ,再证明
,再证明![]() ,即可得出结论.
,即可得出结论.
(1)①如图2中,
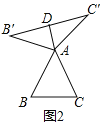
![]() 是等边三角形,
是等边三角形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
故答案为![]() .
.
②如图3中,
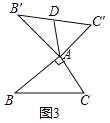
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
故答案为4.
![]() 结论:
结论:![]() .
.
理由:如图1中,延长AD到M,使得![]() ,连接
,连接![]() ,
,![]()
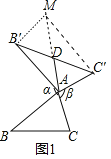
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() .
.
![]() 存在.
存在.
理由:如图4中,延长AD交BC的延长线于M,作![]() 于E,作线段BC的垂直平分线交BE于P,交BC于F,连接PA、PD、PC,作
于E,作线段BC的垂直平分线交BE于P,交BC于F,连接PA、PD、PC,作![]() 的中线PN.
的中线PN.
连接DF交PC于O.

![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]()
易证![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() 四边形CDPF是矩形,
四边形CDPF是矩形,
![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 是
是![]() 的“旋补三角形”,
的“旋补三角形”,
![]() .
.
![]() 的“旋补中线”长
的“旋补中线”长![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点B、F、C、E在同一条直线上,AB∥DE,∠A=∠D,BF=EC.
(1)求证:△ABC≌△DEF.
(2)若∠A=120°,∠B=20°,求∠DFC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某公路检测中心在一事故多发地带安装了一个测速仪,检测点设在距离公路10m的A处,测得一辆汽车从B处行驶到C处所用的时间为0.9秒.已知∠B=30°,∠C=45°

(1)求B,C之间的距离;(保留根号)
(2)如果此地限速为80km/h,那么这辆汽车是否超速?请说明理由.(参考数据:
 ,
, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 经过点
经过点 和点
和点 .
. 求该抛物线所对应的函数解析式;
求该抛物线所对应的函数解析式; 该抛物线与直线
该抛物线与直线 相交于C、D两点,点P是抛物线上的动点且位于x轴下方,直线
相交于C、D两点,点P是抛物线上的动点且位于x轴下方,直线 轴,分别与x轴和直线CD交于点M、N.
轴,分别与x轴和直线CD交于点M、N. 连结PC、PD,如图1,在点P运动过程中,
连结PC、PD,如图1,在点P运动过程中, 的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;
的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由; 连结PB,过点C作
连结PB,过点C作 ,垂足为点Q,如图2,是否存在点P,使得
,垂足为点Q,如图2,是否存在点P,使得 与
与 相似?若存在,求出满足条件的点P的坐标;若不存在,说明理由.
相似?若存在,求出满足条件的点P的坐标;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠CGE=2∠DFB,其中正确的结论有( )个.

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解下列方程.
(1)(6x-1)2-25=0; (2)(3x-2)2=x2;
(3)x2+
 =
= x; (4)(x+1)(x-1)+2(x+3)=8.
x; (4)(x+1)(x-1)+2(x+3)=8. -
科目: 来源: 题型:
查看答案和解析>>【题目】某博物馆每周都吸引大量中外游客前来参观,如果游客过多,对馆中的珍贵文物会产生不利影响,但同时考虑到文物的修缮和保存费用问题,还要保证一定的门票收入,因此,博物馆采取了涨浮门票价格的方法来控制参观人数,在该方法实施过程中发现:每周参观人数与票价之间存在着如图所示的一次函数关系.在这种情况下,如果要保证每周
 万元的门票收入,那么每周应限定参观人数是多少?门票价格应是多少.
万元的门票收入,那么每周应限定参观人数是多少?门票价格应是多少.
相关试题

