搜索
【题目】已知不等臂跷跷板AB长为4米，如图1，当AB的一端A碰到地面时，AB与地面的夹角为α，如图2，当AB的另一端B碰到地面时，AB与地面的夹角为β，已知α=30°，β=37°，求跷跷板AB的支撑点O到地面的高度OH（sin37°=0.6，cos37°=0.8，tan37°=0.75）．
参考答案：
【答案】
米
【解析】
试题分析：根据三角函数的知识分别用OH表示出AO，BO的长，再根据不等臂跷跷板AB长4米，即可列出方程求解即可．
解：根据题意得：AO=OH÷sinα，BO=OH÷sinβ，
AO+BO=OH÷sinα+OH÷sinβ，
即OH÷sinα+OH÷sinβ=4，
则OH=
=
=
=
（米）．
即故跷跷板AB的支撑点O到地面的高度OH是米．
-
科目： 来源： 题型：
查看答案和解析>>【题目】﹣2的绝对值是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若n（其中n≠0）是关于x的方程x2+mx+2n=0的根，则m+n的值为
-
科目： 来源： 题型：
查看答案和解析>>【题目】某学校要招聘一名教师，分笔试和面试两次考试，笔试、面试和最后得分的满分均为100分，竞聘教师的最后得分按笔试成绩：面试成绩＝3∶2的比例计算．在这次招聘考试中，某竞聘教师的笔试成绩为90分，面试成绩为80分，则该竞聘教师的最后成绩是( )
A. 43分 B. 85分 C. 86分 D. 170分
-
科目： 来源： 题型：
查看答案和解析>>【题目】有3张扑克牌，分别是红桃3、红桃4和黑桃5．把牌洗匀后甲先抽取一张，记下花色和数字后将牌放回，洗匀后乙再抽取一张．
（1）列表或画树状图表示所有取牌的可能性；
（2）甲、乙两人做游戏，现有两种方案：A方案：若两次抽得相同花色则甲胜，否则乙胜；B方案：若两次抽得数字和为奇数则甲胜，否则乙胜．请问甲选择哪种方案获胜概率更高？
-
科目： 来源： 题型：
查看答案和解析>>【题目】“校园手机”现象越来越受到社会的关注．“寒假”期间，某校小记者随机调查了某地区若干名学生和家长对中学生带手机现象的看法，统计整理并制作了如下的统计图：
（1）求这次调查的家长人数，并补全图1；
（2）求图2中表示家长“赞成”的圆心角的度数；
（3）已知某地区共6500名家长，估计其中反对中学生带手机的大约有多少名家长？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，直线y1=x+m与双曲线y2=
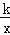交于点A、B，已知点A、B的横坐标为2和﹣1．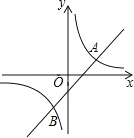
（1）求k的值及直线与x轴的交点坐标；
（2）直线y=2x交双曲线y=
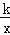于点C、D（点C在第一象限）求点C、D的坐标；（3）设直线y=ax+b与双曲线y=
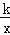（ak≠0）的两个交点的横坐标为x1、x2，直线与 x轴交点的横坐标为x0，结合（1）、（2）中的结果，猜想x1、x2、x0之间的等量关系并证明你的猜想．
相关试题
