【题目】如图,△ABC中,以BC为直径的圆交AB于点D,∠ACD=∠ABC. 
(1)求证:CA是圆的切线;
(2)若点E是BC上一点,已知BE=6,tan∠ABC= ![]() ,tan∠AEC=
,tan∠AEC= ![]() ,求圆的直径.
,求圆的直径.
参考答案:
【答案】
(1)证明:∵BC是直径,
∴∠BDC=90°,
∴∠ABC+∠DCB=90°,
∵∠ACD=∠ABC,
∴∠ACD+∠DCB=90°,
∴BC⊥CA,∴CA是圆的切线
(2)解:在Rt△AEC中,tan∠AEC= ![]() ,
,
∴ ![]() =
= ![]() ,
,
EC= ![]() AC,
AC,
在Rt△ABC中,tan∠ABC= ![]() ,
,
∴ ![]() =
= ![]() ,
,
BC= ![]() AC,
AC,
∵BC﹣EC=BE,BE=6,
∴ ![]() ,
,
解得:AC= ![]() ,
,
∴BC= ![]() ×
× ![]() =10,
=10,
答:圆的直径是10
【解析】(1)根据圆周角定理BC得到∠BDC=90°,推出∠ACD+∠DCB=90°,即BC⊥CA,即可判断CA是圆的切线;(2)根据锐角三角函数的定义得到tan∠AEC= ![]() ,tan∠ABC=
,tan∠ABC= ![]() ,推出AC=
,推出AC= ![]() EC,BC=
EC,BC= ![]() AC,代入BC﹣EC=BE即可求出AC,进一步求出BC即可.
AC,代入BC﹣EC=BE即可求出AC,进一步求出BC即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=﹣2x经过点P(﹣2,a),点P关于y轴的对称点P′在反比例函数
 (k≠0)的图象上.
(k≠0)的图象上. 
(1)求a的值;
(2)直接写出点P′的坐标;
(3)求反比例函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据第五次、第六次全国人口普查结果显示:某市常住人口总数由第五次的400万人增加到第六次的450万人,常住人口的学历状况统计图如下(部分信息未给出):

解答下列问题:
(1)计算第六次人口普查小学学历的人数,并把条形统计图补充完整;
(2)第六次人口普查结果与第五次相比,该市常住人口中高中学历人数增长的百分比是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】目前“自驾游”已成为人们出游的重要方式.“五一”节,林老师驾轿车从舟山出发,上高速公路途经舟山跨海大桥和杭州湾跨海大桥到嘉兴下高速,其间用了4.5小时;返回时平均速度提高了10千米/小时,比去时少用了半小时回到舟山.
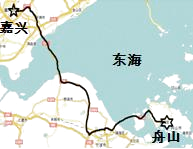
(1)求舟山与嘉兴两地间的高速公路路程;
(2)两座跨海大桥的长度及过桥费见下表:大桥名称
舟山跨海大桥
杭州湾跨海大桥
大桥长度
48千米
36千米
过桥费
100元
80元
我省交通部门规定:轿车的高速公路通行费y(元)的计算方法为:y=ax+b+5,其中a(元/千米)为高速公路里程费,x(千米)为高速公路里程(不包括跨海大桥长),b(元)为跨海大桥过桥费.若林老师从舟山到嘉兴所花的高速公路通行费为295.4元,求轿车的高速公路里程费a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连接这四个点,得四边形EFGH.

(1)如图1,当四边形ABCD为正方形时,我们发现四边形EFGH是正方形;如图2,当四边形ABCD为矩形时,请判断:四边形EFGH的形状(不要求证明);
(2)如图3,当四边形ABCD为一般平行四边形时,设∠ADC=α(0°<α<90°),
①试用含α的代数式表示∠HAE;
②求证:HE=HG;
③四边形EFGH是什么四边形?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=kx+3(k<0)分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,设运动时间为t秒.

(1)当k=﹣1时,线段OA上另有一动点Q由点A向点O运动,它与点P以相同速度同时出发,当点P到达点A时两点同时停止运动(如图1).
①直接写出t=1秒时C、Q两点的坐标;
②若以Q、C、A为顶点的三角形与△AOB相似,求t的值.
(2)当 时,设以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D(如图2),
时,设以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D(如图2),
①求CD的长;
②设△COD的OC边上的高为h,当t为何值时,h的值最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,C是AB延长线上一点,BC=OB,CE是⊙O的切线,切点为D,过点A作AE⊥CE,垂足为E,则CD:DE的值是( )

A.
B.1
C.2
D.3
相关试题

