【题目】如图(1):△ABC中,∠B、∠C的平分线相交于点O,过点O作EF∥BC分别交AB、AC于E、F. 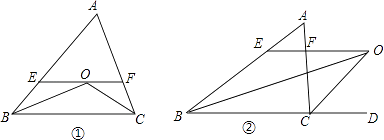
(1)EF与BE、CF之间有什么关系?(不证明)
(2)若△ABC中,∠B的平分线与三角外角∠ACD的平分线CO交于点O,过点O作OE∥BC交AB于E,交AC于F(图示),EF与BE,CF之间又有怎样的数量关系,并给予证明.
参考答案:
【答案】
(1)解:EF=BE+CF.
证明:∵BO平分∠ABC,
∴∠EBO=∠OBC,
∵EF∥BC,
∴∠EDB=∠OBC,
∴∠EOB=∠EBO,
∴OE=BE,
同理CF=OF,
∴EF=OE+OF=BE+CF,
即BE+CF=EF
(2)解:EF=BE﹣CF.
证明:∵BO平分∠ABC,
∴∠EBO=∠CBO,
∴BE=OE,
同理:CF=OF,
∴EF=OE﹣OF=BE﹣CF
【解析】(1)根据角平分线定义和平行线性质求出∠EOB=∠EBO,推出OE=BE,同理得出CF=OF,即可求出答案.(2)结合图形特点,根据(1)中规律,EF=BE﹣CF.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.
-
科目: 来源: 题型:
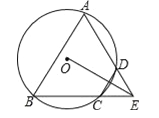
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接四边形,AD的延长线与BC的延长线相交于点E,DC=DE.
(1)求证:∠A=∠AEB;
(2)如果DC⊥OE,求证:△ABE是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面图形上的任意两点P,Q,如果经过某种变换(如:平移、旋转、轴对称等)得到新图形上的对应点P′,Q′,保持P P′= Q Q′,我们把这种对应点连线相等的变换称为“同步变换”。对于三种变换: ①平移、②旋转、③轴对称,其中一定是“同步变换”的有(填序号)。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程是一元二次方程的是( )
A.ax2+bx+c=0B.x2+2x=x2﹣1C.(x﹣1)(x﹣3)=0D.x=2
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明有5张写着不同数字的卡片,请按要求抽出卡片,完成下列各问题:

(1)从中取出2张卡片,使这2张卡片上数字的乘积最大,如何抽取?最大值是多少?答:我抽取的2张卡片是、 , 乘积的最大值为 .
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,如何抽取?最小值是多少?答:我抽取的2张卡片是、 , 商的最小值为 .
(3)从中取出4张卡片,用学过的运算方法,使结果为24。如何抽取?写出运算式子。(写出一种即可)。答:我抽取的4张卡片是、、、 ,
算24的式子为. -
科目: 来源: 题型:
查看答案和解析>>【题目】“同位角相等”,这是______事件(选填“随机”或“必然”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAD=∠DAC,DF⊥AB,DM⊥AC,AF=10cm,AC=14cm,动点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.

(1)求证:在运动过程中,不管t取何值,都有S△AED=2S△DGC .
(2)当t取何值时,△DFE与△DMG全等.
相关试题

