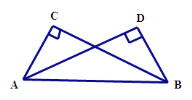
【题目】如图,已知∠ACB=∠BDA=90°,要使△ACB≌△BDA,还需要添加什么条件?请选择一个加以证明
添加:
选择:
证明:
参考答案:
【答案】∠CAB=∠DBA或∠CBA=∠DAB或CA=DB或BC=AD;∠CAB=∠DBA(答案不唯一),证明见解析
【解析】
根据全等三角形的各个判定定理即可得出结论,然后任取其一证明即可.
解:∵∠ACB=∠BDA=90°,AB=BA
∴若添加∠CAB=∠DBA,利用AAS即可证出△ACB≌△BDA;
若添加∠CBA=∠DAB,利用AAS即可证出△ACB≌△BDA;
若添加CA=DB,利用HL即可证出△ACB≌△BDA;
若添加BC=AD,利用HL即可证出△ACB≌△BDA;
如选择∠CAB=∠DBA
证明:在△ACB和△BDA中
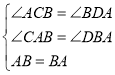
∴△ACB≌△BDA
故答案为:∠CAB=∠DBA或∠CBA=∠DAB或CA=DB或BC=AD;∠CAB=∠DBA(答案不唯一)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.

(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小文想用一张长方形白铁皮做一个长方体无盖盒子,她采取了如下图所示的一个方案(阴影部分是被剪掉的材料,形状为四个相同的正方形).
(1)这块白铁皮的总面积是多少?
(2)这个长方体盒子的表面积是多少?
(3)这个长方体盒子的体积是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】为发展电信事业,方便用户,电信公司对移动电话采取不同的收费方式,其中,所使用的“便民卡”与“如意卡”在某市范围内每月(30天)的通话时间x(min)与通话费y(元)的关系如图所示:
(1)分别求出通话费y1,y2与通话时间x之间的函数关系式;
(2)请帮用户计算,在一个月内使用哪一种卡便宜.

-
科目: 来源: 题型:
查看答案和解析>>【题目】通过计算我们知道:
(a-1)(a+1)=a2-1
(a-1)(a2+a+1)=a3-1
(a-1)(a3+a2+a+1)=a4-1
(1)请根据以上计算规律填空:(a-1)(an+an-1+…+a3+a2+a+1)=______
(2)根据上述规律,请你求出32018+32017+…+33+32+3+1的个位上的数字.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,水库大坝的横断面为四边形ABCD,其中AD∥BC,坝顶BC=10米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30°.
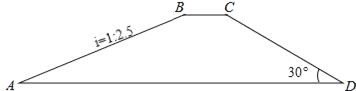
(1)求坝底AD的长度(结果精确到1米);
(2)若坝长100米,求建筑这个大坝需要的土石料(参考数据:
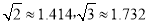 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E是边BC的中点,DE的延长线与AB的延长线相交于点F.
(1)求证:△CDE≌△BFE;
(2)试连接BD、CF,判断四边形CDBF的形状,并证明你的结论

相关试题

